Introduction
La méthode de l'analyse statistique de l'énergie dite méthode SEA (Statistical Energy Analysis) [LYO95] est une approche énergétique qui s'applique aux problèmes d'acoustique et de vibrations hautes fréquences. Elle permet d'estimer les niveaux vibratoires et sonores pour des systèmes complexes tels que les avions, les voitures, les bâtiments, etc.
Le choix d'une méthode de modélisation pour étudier le comportement vibro-acoustique d'un système déformable dépend essentiellement de sa capacité à obtenir des résultats pertinents et fiables dans un temps convenable.
Pour des systèmes présentant des résonances bien séparées, les méthodes déterministes telles que les éléments finis/éléments finis de frontière peuvent calculer en tout point la réponse du système. Ces méthodes s'appliquent généralement aux « basses fréquences ». La limite haute de calcul en fréquence de ces méthodes ne peut être définie de façon stricte car elle est liée à la capacité de l'informatique et à la nature du système étudié. Pour les éléments finis, un critère sur la taille du maillage basé les longueurs d'onde naturelle du système doit être appliqué. Plus on monte en fréquence, plus les longueurs d'onde naturelle sont petites, et plus le nombre de degrés de liberté à considérer dévient important. Il en résulte des temps calculs qui peuvent devenir exorbitants.
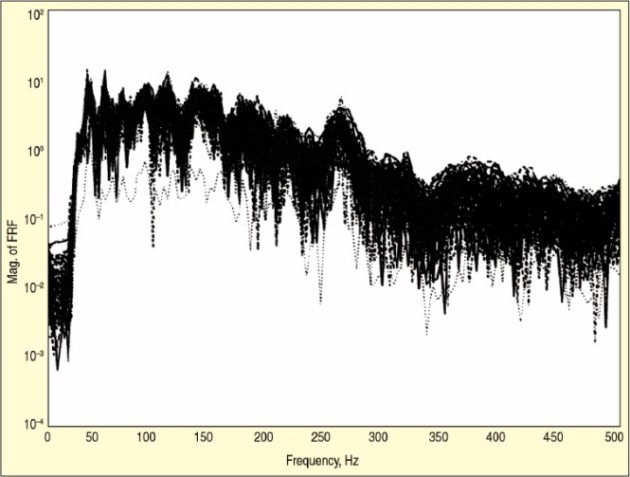
Par ailleurs, en « haute fréquence », il devient illusoire de vouloir prédire de façon déterministe la réponse d'un système. En effet, une dispersion des réponses vibratoires pour des structures apparemment identiques ont pu être observée par différents chercheurs. Leurs travaux ont consisté à mesurer des fonctions de transfert en des points bien définis sur un lot de structures industrielles a priori identiques. Les résultats de ces mesures présentent une forte disparité attribuée à des petites variations non identifiées des caractéristiques des structures considérées (voir un exemple à la figure 1). Cette dispersion semble de plus en plus forte pour les fréquences élevées ce qui rend les méthodes déterministes inopérantes dans les « hautes fréquences ».
Compte tenu de ces limitations des méthodes de discrétisation, une approche plus globale est nécessaire. Au lieu de déterminer la réponse ponctuelle à une fréquence de chaque mode du système étudié, la méthode SEA va chercher à estimer la réponse moyennée dans l'espace, en fréquence et sur une population de structures apparemment identiques d'un ensemble de modes. Sa formulation de base conduit à une méthodologie qui consiste à découper le système global en différents sous-systèmes en respectant un certain nombre d'hypothèses et à traduire les échanges d'énergies vibratoires et acoustiques entre les différents sous-systèmes à partir des équations de base de SEA. Les inconnues caractérisant la réponse du système sont les énergies des sous-systèmes. Leur nombre est alors très faible puis qu'il correspond au nombre de sous-système. La méthode SEA permet donc, moyennant des hypothèses très simplificatrices, d'obtenir facilement des résultats sur le comportement vibro-acoustique de structures relativement complexes, à condition de savoir déterminer les paramètres globaux du modèle.
Les deux principales difficultés sont rencontrées lorsque l'on cherche à appliquer la méthode SEA :
la vérification des nombreuses hypothèses du modèle SEA. Il est nécessaire de bien connaitre les hypothèses du modèle SEA afin de s'assurer au mieux que le système considéré et que la sous-structuration envisagée permettent bien de les vérifier. On tachera au cours de cette présentation du modèle SEA de mettre en lumière les hypothèses posées au fur et à mesure des développements ;
l'estimation des paramètres globaux du modèle, notamment les facteurs caractérisant les transferts d'énergie entre les sous-systèmes que l'on appelle
« facteurs de perte par couplage »
. Différentes approches ont été proposées ces 40 dernières années notamment pour estimer ces facteurs pour des systèmes académiques telles que des poutres, des plaques, des coques. La formulation de base proposée ici donne également une technique pour calculer ces facteurs à partir des modes des sous-systèmes que l'on peut calculer par éléments finis.
On propose de décomposer en trois parties distinctes la formulation permettant d'aboutir au modèle SEA :
la première porte sur l'établissement de relations énergétiques pour un oscillateur isolé ou pour deux oscillateurs couplés entre eux. Ces relations serviront de « briques élémentaires » au modèle SEA. Elles ne feront pas l'objet de démonstration mais on indiquera les hypothèses utilisées pour les obtenir ;
la seconde partie donne les résultats de la double formulation modale. Cette formulation permet de décrire le comportement vibro-acoustique de deux sous-systèmes continus couplés à partir des modes des sous-systèmes. Le schéma de couplage modal obtenu avec cette formulation permet d'associer chaque mode de sous-système au comportement d'un oscillateur. Par ailleurs, les interactions entre ces modes (i.e. oscillateurs) ne font pas apparaître de couplage entre les modes d'un même sous-système.
la dernière partie consiste à effectuer un bilan énergétique pour chaque mode apparaissant dans la double formulation modale (partie 2) en s'appuyant sur les relations énergétiques établies sur des oscillateurs (partie 1). L'hypothèse d'équirépartition des énergies modales est alors introduite pour décrire globalement le comportement des modes d'un même sous-système.
N.B. : Pour les parties 2 et 3, la formulation est proposée en considérant deux sous-systèmes mécaniques couplés. Elle s'étend aisément à un nombre quelconque de sous-systèmes. Elle s'applique également lorsqu'un ou des sous-systèmes sont des milieux acoustiques (par exemple pour étudier le couplage structure-cavité).







