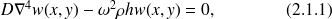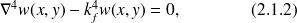Ondes de flexion dans la plaque
Le comportement dynamique des plaques minces est décrit à partir des hypothèses de Love-Kirchhoff :
l'influence du cisaillement transversal (déformation des sections) est négligeable,
l'influence de l'inertie de rotation est négligeable.
On considère que le déplacement transversal est harmonique de pulsation
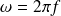et la notation complexe est employée :
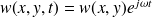
ce qui aura pour conséquence directe d'exprimer l'accélération par :
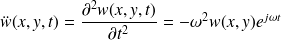
Attention :
En général, le terme
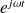est omis dans les équations du mouvement suivantes.
L'équation des vibrations de flexion des plaques minces isotropes est :
|
avec
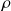la masse volumique de la plaque et
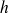son épaisseur.
La constante
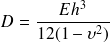correspond à la rigidité de flexion (
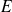module de Young et
coefficient de Poisson) et l'opérateur
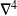est le double Laplacien.
Dans le cas d'un champ en deux dimensions (
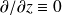), le double Laplacien (aussi noté
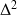) s'obtient par :
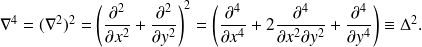
L'équation du mouvement (2.1.1) prend la forme :
|
avec
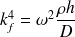, le nombre d'onde des ondes de flexion de la plaque dans le vide.
Si on considère que :
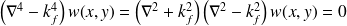
peut se séparer en deux équations :
la solution générale recherchée sera la somme
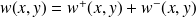des solutions des deux équations :
Ondes propagatives :
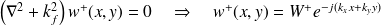,Ondes évanescentes :
.
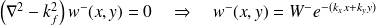Les composantes du vecteur d'onde doivent satisfaire la relation de dispersion :
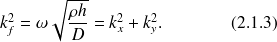
Remarque :
L'équation des ondes peut également s'écrire sous la forme de variables séparées (par exemple pour l'onde propagative) :
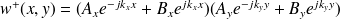avec
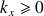et
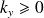
ou encore en considérant un angle
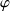pour la direction de propagation de l'onde flexion plane, tel que
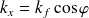et
:
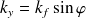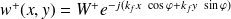
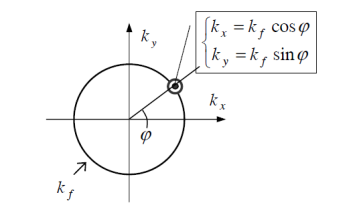
Il est alors possible de définir un plan des nombres d'onde
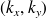où l'onde se propageant dans la direction
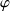sera représentée par un point.
Remarque :
Si on considère la présence d'une excitation dans le domaine spatial étudié, elle se représente par une distribution de force mécanique extérieure au second membre de l'équation du mouvement :
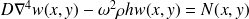ou
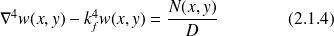
où
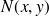est la densité de force répartie sur la surface de la plaque (en
, donc une pression).
Remarque :
Quel que soit le type d'onde, propagatives (
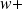) ou évanescentes (
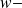), le rapport
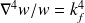fait apparaître le nombre d'onde
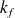. Quand la plaque sera chargée par un fluide lourd, les mêmes fonctions seront présentes avec un nombre d'onde modifié
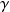. Ce nombre d'onde effectif
de la plaque pourra être obtenu en considérant l'équation (2.1.4) sous la forme :
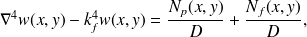
où
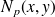est la densité de force due à la fluctuation dynamique du fluide (par exemple la différence de pression pariétale de part et d'autre de la plaque) et
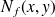est la densité des forces mécaniques extérieures appliquées à la plaque (par exemple
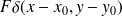pour une force ponctuelle appliquée en
).
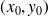En mettant cette équation sous la forme équivalente :
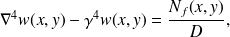
il est possible de définir le nombre d'onde effectif, en dehors des zones d'excitation par les forces extérieures où la pseudo-équation homogène
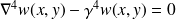est vérifiée :
