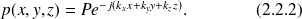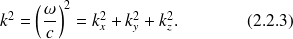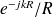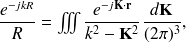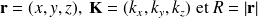Ondes acoustiques dans l'espace semi-infini
Les ondes acoustiques harmoniques dans le milieu semi-infini "au-dessus" de la plaque sont les solutions de l'équation de Helmholtz
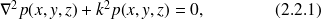
avec le nombre d'onde
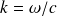 , et dont la forme générale est une onde plane élémentaire (2.2.2) :
, et dont la forme générale est une onde plane élémentaire (2.2.2) :
|
Pour vérifier l'équation (2.2.1), les composantes
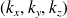 du vecteur d'onde doivent aussi satisfaire la relation de dispersion (2.2.3)
du vecteur d'onde doivent aussi satisfaire la relation de dispersion (2.2.3)
|
La solution (2.2.2) peut aussi s'écrire sous la forme équivalente (variables séparées) :
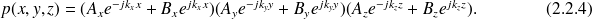
Si la pression dans le demi-espace
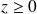 est due au rayonnement de la plaque située dans le plan
est due au rayonnement de la plaque située dans le plan
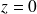 , le terme
, le terme
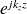 qui correspond à une onde plane se propageant vers la plaque ne correspond pas à une réalité physique. La pression peut donc être décrite par :
qui correspond à une onde plane se propageant vers la plaque ne correspond pas à une réalité physique. La pression peut donc être décrite par :

en représentant par
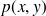 la pression dans le plan
la pression dans le plan
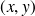 en
en
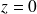 .
.
Si les variables
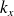 et
et
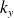 sont imposées par la pression
sont imposées par la pression
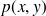 sur le plan
sur le plan
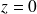 , la relation de dispersion (2.2.3) montre que la variable
, la relation de dispersion (2.2.3) montre que la variable
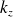 n'est pas indépendante :
n'est pas indépendante :
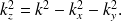
Pour illustrer cette condition simplement, on considère un champ pour lequel
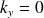 (c'est à dire
(c'est à dire
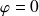 ), soit
), soit
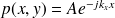 . Ecrire
. Ecrire
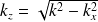 revient à définir l'orientation de l'onde plane par rapport à l'axe
revient à définir l'orientation de l'onde plane par rapport à l'axe
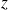 sous la forme d'un angle
sous la forme d'un angle
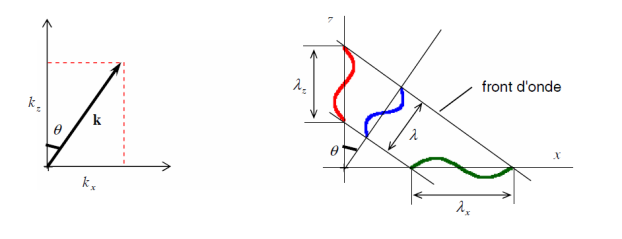
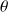 . Le vecteur d'onde de module
. Le vecteur d'onde de module
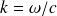 se projette selon les composantes :
se projette selon les composantes :
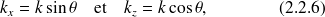
comme le montre la Figure 2.2.
Dans le domaine spatial la répartition de la pression sur les axes
 et
et
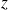 est représentée par les composantes des longueurs d'onde :
est représentée par les composantes des longueurs d'onde :

où
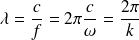 .
.
La trace de l'onde plane (2.2.2) sur un plan à
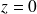 peut se représenter dans le domaine des nombres d'onde, par un spectre dans un plan
peut se représenter dans le domaine des nombres d'onde, par un spectre dans un plan
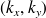 . L'onde plane de l'exemple précédent se représente par un point en
. L'onde plane de l'exemple précédent se représente par un point en
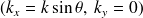 du domaine des nombres d'onde.
du domaine des nombres d'onde.
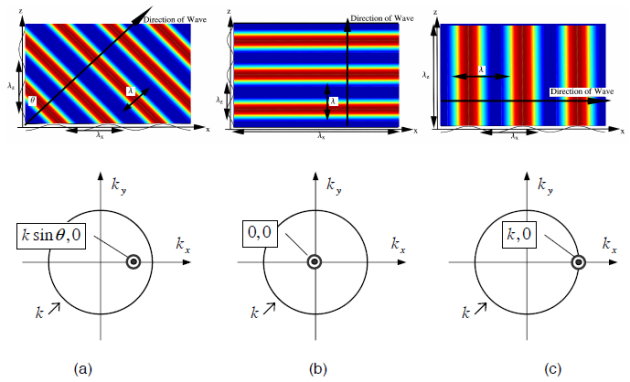
La Figure 2.3 représente l'onde plane dans l'espace
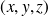 et dans le domaine
et dans le domaine
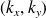 pour :
pour :
le cas général de l'onde dans une direction
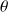 ,
,l'onde dans la direction normale :
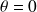 et
et
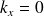 ,
,l'onde dans la direction rasante :
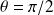 et
et
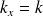 .
.
Pour une onde plane dont la direction de propagation projetée sur le plan
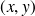 présente un angle
présente un angle
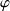 par rapport à la direction
par rapport à la direction
 , le spectre de nombre d'onde est représenté par un point en :
, le spectre de nombre d'onde est représenté par un point en :
Remarque :
Si le demi-espace
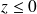 est considéré, alors c'est le terme
est considéré, alors c'est le terme
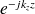 qui correspond à une onde plane se propageant vers la plaque et qui est supprimé. La pression dans ce demi-espace est donc :
qui correspond à une onde plane se propageant vers la plaque et qui est supprimé. La pression dans ce demi-espace est donc :