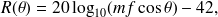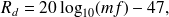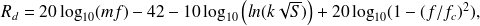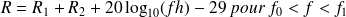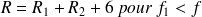Transparence acoustique des doubles parois

En gardant un comportement de masse pour les parois, des modèles simples ont été développés pour prédire la transparence acoustique des parois simples et doubles. L'indice d'affaiblissement d'une plaque soumise à une onde plane à incidence normale prévoit ainsi une croissance de l'indice d'affaiblissement de 6dB par octave :

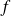avec la masse surfacique , la fréquence (Hz), et 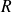l'indice d'affaiblissement (dB). Cependant, cette loi de masse ne tient compte ni de la fréquence critique ni de l'excitation en champ diffus. De nouvelles expressions ont donc été proposées : la loi de masse pour une plaque excitée par une onde plane avec un angle d'incidence 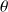(Eq.(35)), la loi de masse en champ diffus (Eq.(36)), la loi de masse en champ diffus corrigée par Sewell pour prendre en compte les dimensions finies de la plaque en dessous de la fréquence critique (Eq.(37)), et la loi de masse en champ diffus corrigée par Cremer au dessus de la fréquence critique (Eq.(38)) :

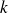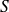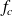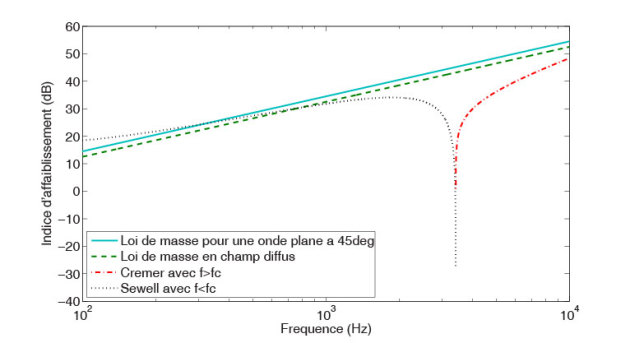
avec le nombre d'onde, la surface de la plaque, sa masse surfacique, sa fréquence critique, et 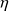son amortissement structural. Les résultats obtenus à l'aide de ces différentes expressions sont présentés sur la figure (5) pour une simple plaque en aluminium de 3.5mm d'épaisseur.

FIGURE 5 – Illustrations des différents modèles basés sur la loi de masses pour une simple plaque en aluminium de 3.5mm d'épaisseur

Le cas des doubles parois a ensuite été étudié de façon similaire par Sharp. Il décompose le comportement de la double paroi en trois zones fréquentielles :

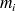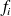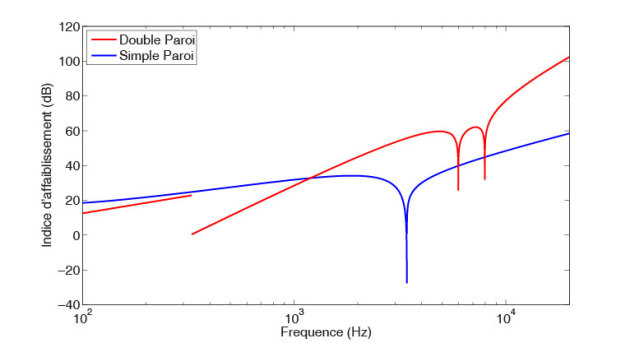
avec la fréquence de respiration, d la distance entre les deux parois, les masses surfaciques des plaques, les fréquences critiques des plaques, et 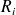les indices d'affaiblissement des plaques calculés avec le modèle de Cremer. En dessous de la fréquence de respiration, l'indice d'affaiblissement croît de 6dB par octave, puis il augmente de 18dB par octave jusqu'à la fréquence critique minimale des plaques où se produit une nette diminution de l'isolation acoustique. Ensuite, au-dessus des fréquences critiques il continue d'augmenter de 18dB par octave. Il faut néanmoins noter que les premières résonances de la cavité ont tendance à diminuer l'isolation des doubles parois et lorsqu'elles se produisent, la croissance de l'indice d'affaiblissement est alors ramenée à 12dB par octave. La figure (6) présente une comparaison de l'indice d'affaiblissement entre une double paroi et une simple paroi de masse équivalente. Ces courbes nous montrent bien l'intérêt de la double paroi en haute fréquence, et son inefficacité en basse fréquence.

FIGURE 6 – Cas de la double paroi en aluminium de 1.5mm et 2mm d'épaisseur séparée par 1cm d'air (en rouge) et comparaison avec une simple paroi équivalente de 3.5mm d'épaisseur (en bleu)