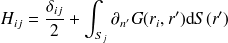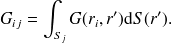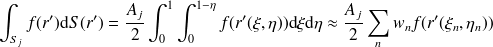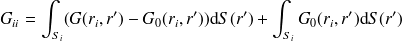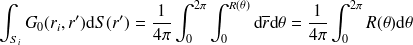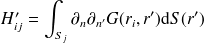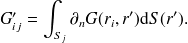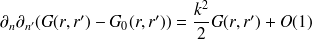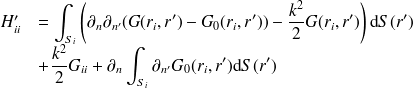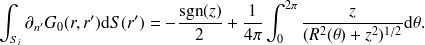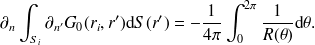Les éléments constants
La discrétisation la plus simple est de considérer les champs constants sur chaque élément de surface. Notons qu'une approximation aussi grossière n'est pas possible avec la méthode des éléments finis, elle est toutefois envisageable dans le cas des équations intégrales. Simplifions encore l'analyse en prenant comme élément des surfaces triangulaires planes. On choisit les points de collocation
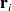au barycentre du triangle, ainsi on pose
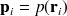et
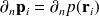. Les coefficients des matrices
et
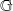se calculent à partir de :
| (44) |
Deux scénarios s'imposent :
(i) si
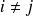, les intégrales sont régulières et on peut utiliser les formules de quadrature de Gauss-Legendre :
| (45) |
où
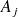désigne l'aire du triangle
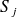. En pratique, la sommation sur
est en général limitée à quelques points d'intégration (de 3 à 8).
(ii) si
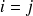, on a simplement
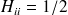, par contre la deuxième intégrale est faiblement singulière. On peut soustraire la singularité en faisant
| (46) |
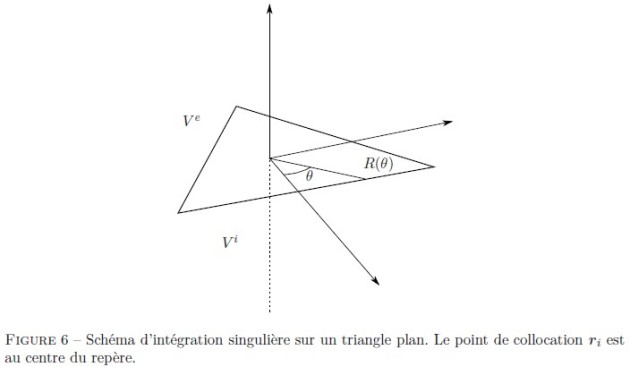
puis en coordonnées polaires (voir Fig. 6), on régularise la deuxième intégrale :
| (47) |
Rappelons que dans le système de coordonnées locales
,
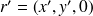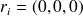est le centre du repère et
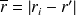(voir Fig. 6). On peut trouver une solution exacte de (47) dans [1] ou bien utiliser un schéma d'intégration classique.
Les coefficients non diagonaux
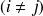des matrices
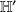et
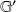se calculent à partir de :
| (48) |
Lorsque
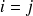on a simplement
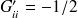par contre le calcul de
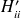est plus délicat. Dans le cas présent, on peu s'affranchir des procédés de régularisation et un calcul direct peut être effectué. Ici encore, on peut soustraire la singularité en observant que
| (49) |
quand
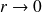. Ceci donne
| (50) |
Dans le système de coordonnées locales (voir Fig. 6),
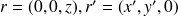. On peut calculer
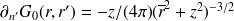. Ainsi, après intégration en coordonnées polaires, on trouve
| (51) |
On peut dériver cette expression puis faire tendre
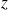vers 0 pour trouver finalement
| (52) |
Pour une structure maillée assez finement, l'approximation par éléments constants donne de bons résultats surtout si on s'intéresse plus particulierement au champ lointain (signature radar, etc...). On peut trouver l'algorithme de calcul (FORTRAN) par élément constant présenté ici dans [1]. Notons enfin qu'en s'inspirant des calculs précédents, on peut retrouver la formule (10).
