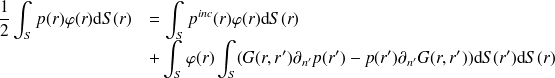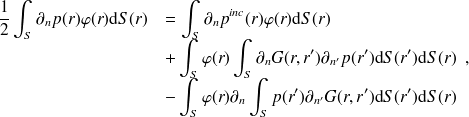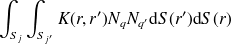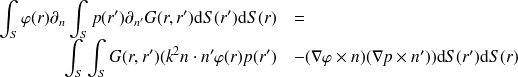Méthode variationnelle
Cela revient à chercher la solution des équations intégrales (9) et (10) de telle sorte que
| (40) |
et
| (41) |
où
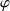est une fonction test assez régulière. Dans l'approche de Galerkin, la fonction test est choisie parmi les fonctions d'approximations utilisées pour le champ de pression et de vitesse (typiquement de la forme (27)). Ce choix a pour conséquence de rendre les matrices symétriques. Le calcul des coefficients des matrices fait intervenir des intégrales double de la forme
| (42) |
où
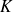désigne
,
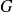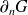ou
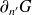. L'intégrale hypersingulière se régularise à l'aide d'un résultat établi par Hamdi [4] :
| (43) |
L'intégrale devient intégrable au sens classique et est du type (42). Des algorithmes d'intégration pour des singularité en
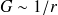abondent dans la littérature, on peut se référer à [10] par exemple.
