Applications pratiques de la SEA

L'utilisation de la SEA pour des applications industrielles (typiquement de l'industrie des transports) est moins aisée que dans l'industrie du bâtiment à cause principalement de la complexité géométrique des systèmes étudiés. En effet, le principal problème pratique est le choix des sous-systèmes SEA respectant des hypothèses restrictives. Cette définition des sous-systèmes est généralement laissée à des « experts » même si des recherches récentes essaient de proposer des méthodes automatiques de détection des sous-systèmes SEA en analysant les réponses du système modélisé par éléments finis [TOT06].

Dans le cas d'application présenté ci-dessous, le tronçon de TGV Duplex présenté en figure 2.10 a été découpé en 8 sous-systèmes définis dans la figure 2.11. Ces sous-systèmes sont censés respecter les hypothèses de la SEA comme le couplage faible entre les sous-systèmes.

Figure 2.10. Exemple d'application industrielle de la SEA : un tronçon de TGV Duplex.

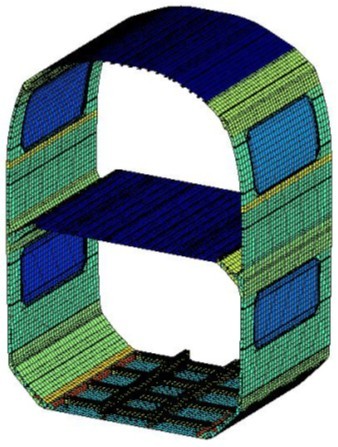
Il faut aussi bien garder en tête que cette sous-structuration « idéale » dépend de la bande de fréquence d'étude et qu'elle ne respecte pas nécessairement un découpage en « pièces » du système. De plus, une mauvaise sous-structuration du système mènera à une mauvaise estimation des échanges d'énergie entre les sous-systèmes.

Figure 2.11. Sous-structuration en 8 sous-systèmes utilisée pour la modélisation du tronçon de TGV Duplex

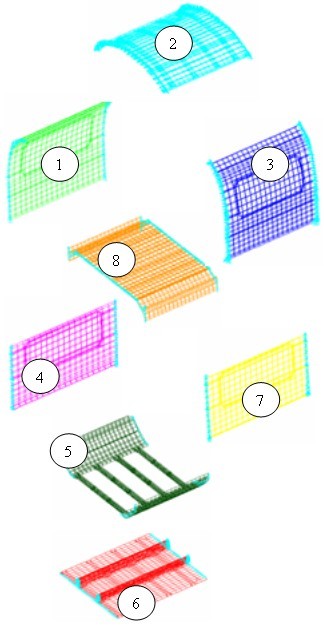
Après avoir déterminé les sous-systèmes SEA, il est nécessaire de calculer les facteurs de perte par couplage entre les sous-systèmes. En utilisant les équations (4.9) et (4.20) présentées dans « La formulation de base du modèle SEA », les facteurs de perte ont pu être calculés à partir des modèles éléments finis des sous-systèmes découplés. Ces facteurs de perte par couplage pour l'octave 250Hz sont présentés en figure 2.12.

Figure 2.12. Facteurs de perte par couplage

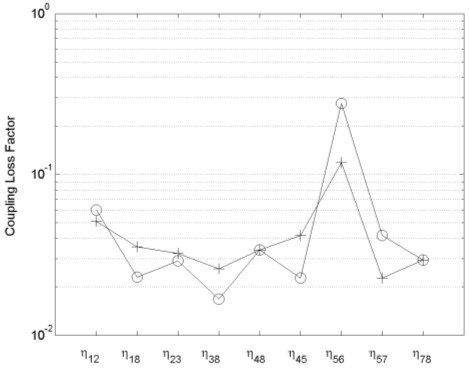
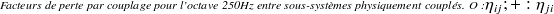
On observe sur la figure 2.12 des facteurs de perte par couplage effectivement assez faibles sauf pour le couplage entre les sous-systèmes S5 et S6 qui sont physiquement très liés. Ces deux sous-systèmes pourraient ainsi dans cette bande de fréquence être éventuellement considérés comme un seul.

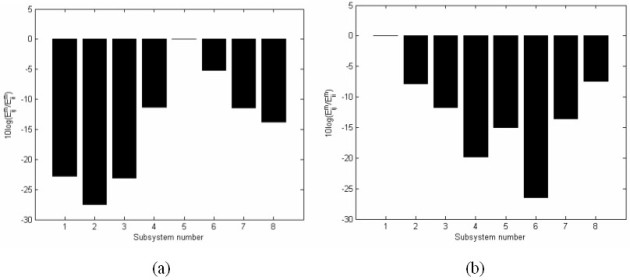
La réponse énergétique des sous-systèmes lorsque l'un d'entre eux est excité peut-être calculée en utilisant le modèle SEA ainsi construit. A la figure 2.12, on présente la réponse des sous-systèmes à deux cas d'excitation : sous-système 5 est excité ou sous-système 1 excité.

Figure 2.12. Rapport d'énergie entre les sous-systèmes et le sous-système excité.(a) Sous-système 5 excité ; (b) sous-système 1 excité. Octave 250Hz.

L'analyse de la figure 2.12 montre que l'atténuation de l'énergie est très forte entre le bas de la structure et son sommet. Ainsi, lorsque le sous-système 5 est excité, le sous-système 2 présente une énergie 27dB plus faible que l'énergie du sous-système 5. Les deux autres sous-systèmes qui répondent le moins à cette excitation sont les sous-systèmes 1 et 3 qui sont placés symétriquement de part et d'autre du sous-système 2. Le sous-système 6 est celui qui est le plus sollicité par cette excitation (hormis le sous-système excité) ce qui est en concordance avec la remarque selon laquelle le facteur de perte par couplage entre les sous-systèmes 5 et 6 est le plus fort dans cette bande de fréquence.