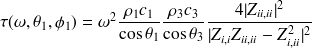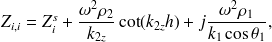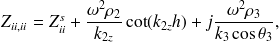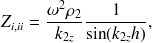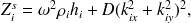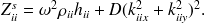Transparence acoustique
En réinjectant les pressions et déplacements dans la formulation globale du problème, nous arrivons à un système d'équations linéaires dont les inconnues sont les amplitudes des ondes transmises et réfléchies dans chaque milieu. L'intensité d'une onde plane propagative étant directement liée au carré de l'amplitude de pression, le rapport énergétique entre la sortie et l'entrée de la double paroi s'écrit donc comme le rapport des pressions transmises dans le dernier milieu et de la pression incidente du premier milieu. Ce rapport correspond à la transparence acoustique de la paroi considérée et s'écrit :
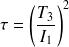. Tout calcul fait, nous obtenons :
| (20) |
avec
| (21) |
| (22) |
| (23) (24) |
et
| (25) |
| (26) |
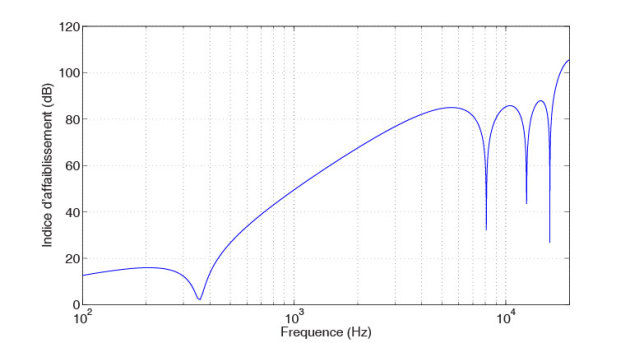
L'indice d'affaiblissement en dB est définit avec le logarithme de la transparence acoustique tel que
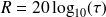. La figure (8) présente cet indice pour une double paroi infinie. On y retrouve les principaux phénomènes décrits par la suite : le phénomène de respiration, le gain théorique de 18dB par octave, les fréquences critiques des plaques, le découplage haute fréquence, ...
