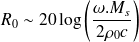Loi de masse
Il est possible dans les basses fréquences de fournir une formule simple de l'indice d'affaiblissement pour une onde acoustique ayant une incidence normale sur la paroi.
| (15) |
avec
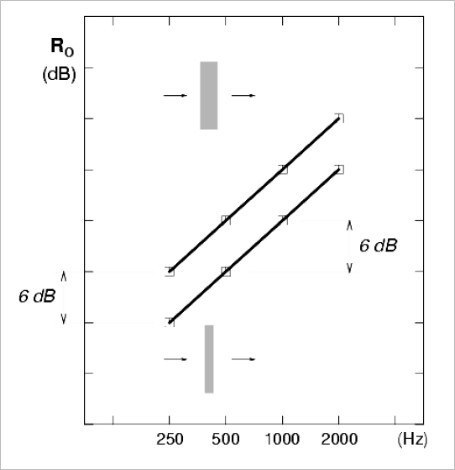
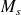la masse par unité de surface de la paroi. Cette approximation est connue sous le nom de loi de masse, car seuls les effets d'inertie sont pris en compte . Malgré sa simplicité, elle fournit une bonne estimation du comportement des parois infinies et même finies. La figure 7 montre que l'atténuation augmente de 6 dB avec le doublement de la masse par unité de surface, mais également de 6 dB chaque fois que la fréquence est doublée (6 dB/octave). Il sera donc difficile d'empêcher la transmission des basses fréquences. Le tableau 2 montre quelques exemples d'indices d'affaiblissement de matériaux communs.
Masse volumique (kg/m3) | Module d'Young (N/m2) | Coefficient de Poisson | Facteur de perte | R0 (dB) à 1000 Hz, h=0.001 m | |
|---|---|---|---|---|---|
Acier | 7800 | 2,1 1011 | 0,28 | 5 10-4 | 35,8 |
Aluminium | 2700 | 7,2 1010 | 0,33 | 10-4 | 26,6 |
Verre | 2500 | 6,25 1010 | 0,22 | 10-3 | 25,9 |
Polycarbonate | 1200 | 2;3 109 | 0,34 | 10-2 | 19,5 |
