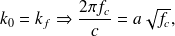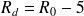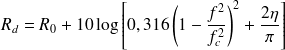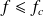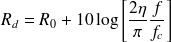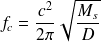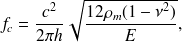Éléments pour l'insonorisation

Le phénomène de coïncidence, qui apparaît pour un angle d'incidence oblique, va provoquer une réduction significative de l'indice d'affaiblissement acoustique à la fréquence de coïncidence. En dessous de cette fréquence, la loi de masse se trouve réduite de 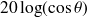, où 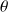est l'angle d'incidence. La fréquence de coïncidence la plus basse correspond à la fréquence critique , fréquence pour laquelle la longueur d'onde de flexion dans le panneau correspond à la longueur d'onde dans l'air (voir expression plus loin) :

où est une constante dépendant des caractéristiques mécaniques de la cloison.

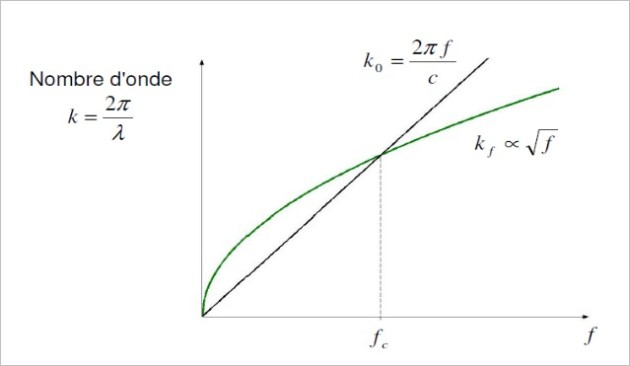
Figure 8 : nombre d'onde de flexion dans un panneau et nombre d'onde acoustique en fonction de la fréquence

Un indice d'affaiblissement en champ diffus est obtenu pour les fréquences inférieures à 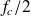en considérant des valeurs inférieures à 5 dB à la loi de masse :

A la fréquence critique , l'isolement passe par un minimum et croit ensuite avec une pente de 9 dB par octave. Le facteur de perte interne de la paroi a seulement une influence à la fréquence critique (voir figure 9).

Figure 9 : indice d'affaiblissement en champ diffus pour une paroi infinie et deux valeurs du facteur de perte.

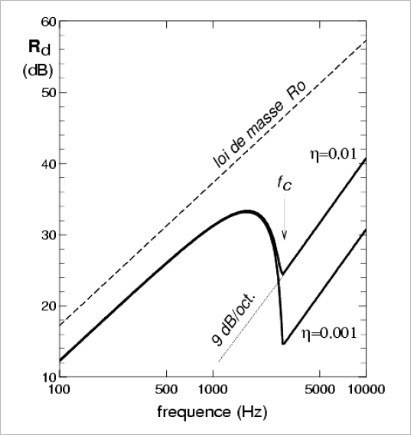
La formule approchée qui est utilisée pour calculer l'indice d'affaiblissement en champ diffus est (voir par exemple [Fahy 1985]) :

En dehors de la masse par unité de surface utilisée pour déterminer la loi de masse 0 R , l'indice d'affaiblissement acoustique en champ diffus d R nécessite de connaître le facteur de perte h du matériau et la fréquence critique de la paroi :

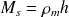Avec et 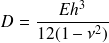on obtient :

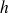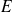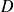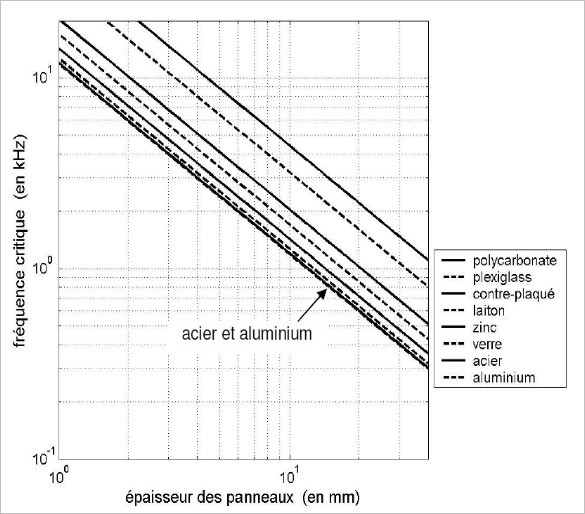
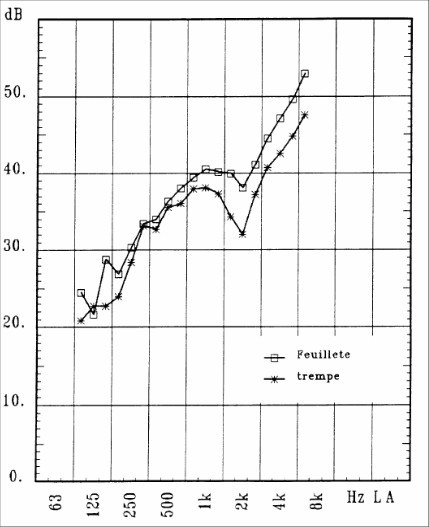
avec la masse volumique du matériau (kg/m³), l'épaisseur de la paroi (m), le coefficient de Poisson, le module d'Young (N/m²), la rigidité de flexion et la célérité du son dans l'air (m/s). La figure 10 montre quelques exemples de fréquences critiques en fonction du matériau et de l'épaisseur de la paroi, la figure 11 illustre des indices d'affaiblissement mesurés sur vitrages.

Figure 10 : fréquences critiques en fonction de l'épaisseur des panneaux pour différents matériaux.

Figure 11 : indices d'affaiblissement de vitrages de 8 mm en verre trempé et en verre feuilleté (échantillons de 0,84 m x 0,84 m, montage par joint à clé en caoutchouc)