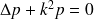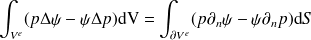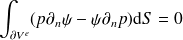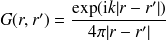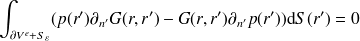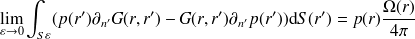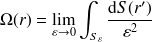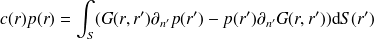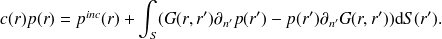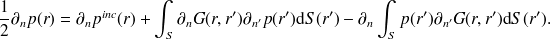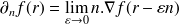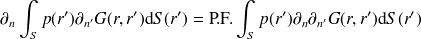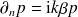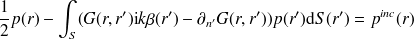Représentation directe
On rappelle que la propagation des ondes acoustiques dans un milieu homogène d'impédance caractéristique
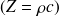 est décrite par l'équation de Helmholtz
est décrite par l'équation de Helmholtz
| (1) |
où
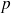 est la pression et
est la pression et
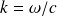 le nombre d'onde. Nous nous intéressons au calcul du champ de pression à l'extérieur d'une structure de surface fermée
le nombre d'onde. Nous nous intéressons au calcul du champ de pression à l'extérieur d'une structure de surface fermée
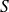 (figure 1). On désigne par
(figure 1). On désigne par
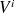 et
et
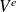 l'intérieur et l'extérieur de l'objet. La surface fictive
l'intérieur et l'extérieur de l'objet. La surface fictive
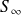 est une sphère de rayon arbitrairement grand.
est une sphère de rayon arbitrairement grand.
Attention :
ici, nous considérons les solutions harmoniques du temps avec la convention
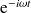 .
.
Pour n'importe quelle fonction régulière
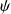 sur
sur
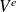 l'application du deuxième théorème de Green donne
l'application du deuxième théorème de Green donne
| (2) |
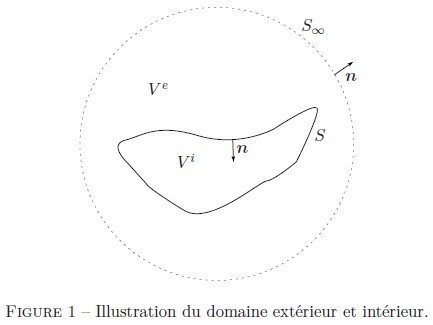
où
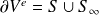 désigne les frontières de
désigne les frontières de
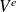 . Ainsi, si
. Ainsi, si
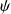 est solution de (1) alors
est solution de (1) alors
| (3) |
On prend maintenant deux points de l'espace
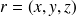 et
et
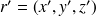 et on définit la fonction de Green
et on définit la fonction de Green
| (4) |
Attention :
Pour la suite de la démonstration, il est essentiel de considérer
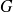 comme une fonction de
comme une fonction de
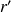 alors que le point
alors que le point
 est fixe.
est fixe.
On voit ainsi que
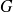 vérifie (1) sauf au point
vérifie (1) sauf au point
 où
où
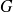 n'est pas définie. Pour contourner la difficulté, on considère une petite surface sphérique notée
n'est pas définie. Pour contourner la difficulté, on considère une petite surface sphérique notée
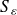 centrée sur
centrée sur
 et de rayon
et de rayon
 . En appliquant (3) alors
. En appliquant (3) alors
| (5) |
Ici,
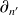 signifie que l'on dérive par rapport à la normale
signifie que l'on dérive par rapport à la normale
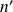 au point
au point
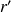 . Notons que lorsque
. Notons que lorsque
 n'est pas sur la frontière du domaine,
n'est pas sur la frontière du domaine,
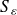 forme une sphère complète alors qu'elle est limitée à un certain secteur angulaire dans le cas où
forme une sphère complète alors qu'elle est limitée à un certain secteur angulaire dans le cas où
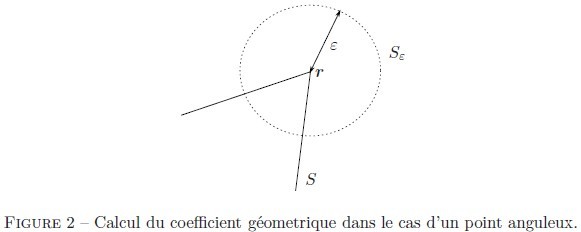
 repose sur le bord de la structure (figure 2). Maintenant, en faisant tendre
repose sur le bord de la structure (figure 2). Maintenant, en faisant tendre
 vers 0, alors
vers 0, alors
| (6) |
où
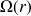 désigne l'angle solide
désigne l'angle solide
| (7) |
Le traitement de l'intégrale sur
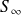 se fait en rappelant que la pression rayonnée doit satisfaire la condition de Sommerfeld :
se fait en rappelant que la pression rayonnée doit satisfaire la condition de Sommerfeld :
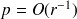 et
et
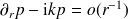 lorsque
lorsque
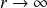 .
.
En observant que la fonction de Green satisfait aussi cette condition, on trouve que l'intégrale sur
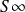 tends vers zéro.
tends vers zéro.
Cela donne
| (8) |
où on a posé
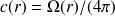 . Ainsi
. Ainsi
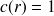 si
si
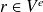 et
et
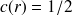 si
si
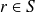 et si la surface est plane au voisinage de
et si la surface est plane au voisinage de
 . On remarque de plus, à partir de (3) qu'on a nécessairement
. On remarque de plus, à partir de (3) qu'on a nécessairement
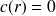 si
si
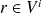 . L'équation (8) se généralise facilement en présence d'un champ incident
. L'équation (8) se généralise facilement en présence d'un champ incident
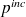 . On obtient finalement
. On obtient finalement
| (9) |
|---|
L'équation (9) est appelée formulation directe. En rappelant que
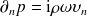 où
où
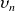 représente la vitesse acoustique normale à la paroi, on voit que les données sur les bords de l'obstacle sont les variables physiques : vitesse et pression. Il est parfois utile d'avoir une formule similaire pour la vitesse acoustique, il faut pour cela dériver (9) selon la normale
représente la vitesse acoustique normale à la paroi, on voit que les données sur les bords de l'obstacle sont les variables physiques : vitesse et pression. Il est parfois utile d'avoir une formule similaire pour la vitesse acoustique, il faut pour cela dériver (9) selon la normale
 au point
au point
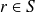 (à condition que la surface soit régulière en ce point). Cette opération n'est pas triviale mais on peut montrer que
(à condition que la surface soit régulière en ce point). Cette opération n'est pas triviale mais on peut montrer que
| (10) |
|---|
Les équations (9) et (10) sont fondamentales et sont à la base de la méthode des éléments de frontière.
Remarque :
La dérivée selon la normale à la surface d'une fonction
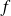 définie dans
définie dans
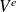 doit être interprétée comme la limite du gradient de la fonction calculé dans
doit être interprétée comme la limite du gradient de la fonction calculé dans
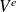 , c'est-à-dire
, c'est-à-dire
| (11) |
pour un point
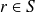 .
.
Remarque :
Notons que l'opérateur de dérivation
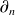 est volontairement laissé à l'extérieur de la deuxième intégrale. En fait on montre que
est volontairement laissé à l'extérieur de la deuxième intégrale. En fait on montre que
| (12) |
L'intégrale de droite est divergente et le signe P.F. signifie qu'il faut calculer cette intégrale au sens de la partie finie de Hadamard. Ce calcul n'est pas simple et doit être mené avec précaution (voir Section 5).
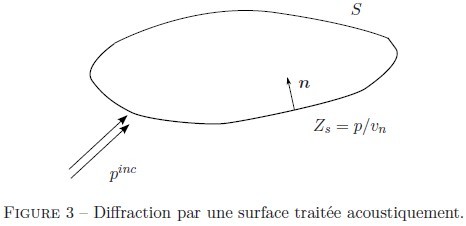
Exemple : Diffraction par une structure localement réactive
On considère une surface traitée acoustiquement avec une impédance localisée
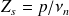 .
.
La condition aux limites sur les bords s'écrit
| (13) |
où on a posé
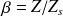 . La formulation directe (9) sur le bord régulier
. La formulation directe (9) sur le bord régulier
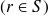 devient
devient
| (14) |