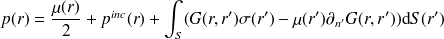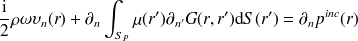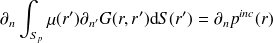Représentation indirecte
La formulation (9) n'est en fait pas unique car il existe d'autres champs de ‘vitesse' et de ‘pression' sur le bord
qui génère le même champ de pression dans
. Pour s'en convaincre, il suffit de considérer la formulation du problème intérieur pour la pression
. L'équation intégrale pour
est identique à (8) :
| (15) |
Cela aboutit, après recombinaison, à la formulation indirecte :
| (16) |
où
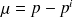est la différence de pression
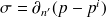le saut de ‘vitesse' de part et d'autre de la plaque. Rappelons que (16) n'est valable que pour un point dans
. Sur le bord régulier (
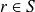et
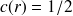), on trouve
| (17) |
De la même façon, en utilisant (10), on trouve un résultat similaire pour la dérivée normale
| (18) |
La relation linéaire reliant
et sa dérivée normale aux sauts
et
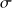forme l'opérateur de Calderón [3].
Exemple : diffraction par une plaque mince
On appele
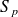la surface de la plaque. On prolonge
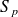par une surface fictive
de telle sorte que
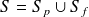soit fermée. Dans ce cas, il est évident que
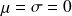sur
. De plus la vitesse acoustique de part et d'autre de la plaque est égale.
Cela revient à poser
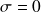sur
.
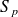On obtient
| (19) |
Dans le cas d'un écran rigide
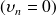, on forme une équation pour le saut de pression
:
| (20) |
De plus champ de pression est continu sur les bords de l'écran
: l'équation (20) doit être résolue en rajoutant la condition
sur
.
