Problème intérieur
Prenons le cas où la pression interne
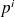est imposée sur les bords (pb de Dirichlet), alors
| (21) |
Cette équation intégrale du premier type est mal conditionnée, on préfère alors appliquer l'équation dérivée :
| (22) |
Cette équation du second type est bien conditionnée grâce au premier terme. Par contre le calcul numérique du terme de droite pose des difficultés pouvant affecter la qualité de la solution. Une solution préconisée dans [1] est de choisir une combinaison judiceuse de ces deux équations. Notons enfin qu'il existe un nombre dénombrable de valeurs de
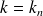pour lesquelles la solution de (22) n'est pas unique : ce sont les modes de résonance de cavité à pression nulle sur les bords. A ces fréquences, l'équation intégrale (22) n'est donc pas inversible. La décomposition de la fonction de Green sur les modes de cavité montre que
lorsque
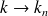, donc on peut anticiper que le conditionnement de (22) se comporte de façon similaire autour de la résonance.
