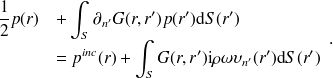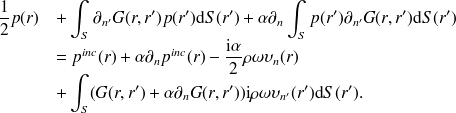Problème extérieur
Prenons maintenant le cas où la vitesse acoustique
est imposée sur les bords de l'obstacle (pb de Neumann), alors
| (23) |
On remarque que cette équation pour la pression est strictement la même que l'équation précédente (22) pour la vitesse ! Par conséquent (23) n'est pas inversible lorsque la fréquence (ou
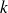) correspond à la résonance du problème intérieur. Ici, la résonance n'a rien de physique mais est inhérente à la formulation intégrale. Numériquement, cela se traduit par un mauvais conditionnement et par conséquent une détérioration de la qualité des résultats autour de la résonance. Parmi les nombreuses techniques éxistantes pour contourner cette difficulté, on peut en citer deux (probablement les plus connues) : la méthode de Schenck [6] et la méthode de Burton & Miller [5].
Méthode : La méthode de Schenck
La méthode consiste à choisir
points internes
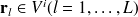et d'appliquer (23) :
| (24) |
On montre que le système d'équations (23) et (24) produit une solution unique. La méthode n'est toutefois pas très précise quand la fréquence augmente. De plus, l'emplacement des points internes doit être judicieusement choisi de telle sorte que ces points ne soient pas trop proches d'une surface nodale du problème intérieur correspondant. Ces surfaces ne sont a priori pas connues ce qui rend la méthode un peu hasardeuse.
Méthode : La méthode de Burton & Miller
Cette méthode consiste à combiner linéairement l'équation originale (23) avec sa dérivée (10).
Cela donne dans le cas présent :
| (25) |
Le coefficient de couplage
doit avoir une partie imaginaire non nulle pour garantir l'unicité de la solution. En pratique
s'avère être un bon choix.
