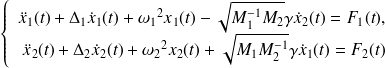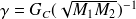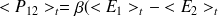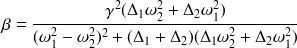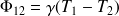Puissance échangée par deux oscillateurs couplés par un élément gyroscopique
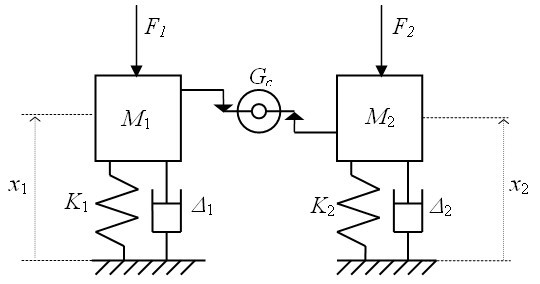
Deux oscillateurs couplés via un élément « gyroscopique » sont considérés (voir figure 3).
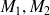sont les inerties,
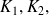les raideurs. Chaque oscillateur est lié à un amortisseur visqueux de bande d'amortissement :
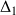pour l'oscillateur 1 et
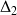pour l'oscillateur 2. Par ailleurs, ces deux oscillateurs sont excités par des efforts extérieurs
.
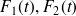L'élément « gyroscopique » est un système mécanique particulier ayant les propriétés suivantes :
Les forces de couplage transmises à travers l'élément de couplage gyroscopique sont proportionnelles aux vitesses des deux masses,
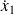et
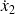. On note
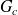, la constante de proportionnalité ;Il se comporte de telle façon que lorsque la vitesse de l'oscillateur 1 est positive, la force appliquée sur l'oscillateur 2 est négative, et que lorsque la vitesse de l'oscillateur 2 est positive, la force appliquée sur l'oscillateur 1 reste positive.
Bien que les efforts induits par cet élément soient proportionnels aux vitesses des inerties, il ne dissipe pas d'énergie (ce que l'on pourra vérifier par un bilan de puissance). On parle dans la littérature d'un couplage de type gyroscopique ou gyrostatique. Néanmoins, il ne présente pas de réalité physique. On considère ce type de liaison entre les 2 oscillateurs plutôt qu'un couplage plus classique en masse et raideur car on verra que seul celui-ci intervient dans le schéma de couplage modal issu de la double formulation modale (voir partie 2).
On rappelle que les pulsations propres des oscillateurs découplés sont données par :
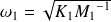pour l'oscillateur 1 et
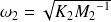pour l'oscillateur 2.
Les équations du mouvement des deux oscillateurs couplés et excités par les forces extérieures
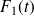et
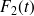peuvent s'écrire sous la forme :
| (2.13) |
où le coefficient de couplage gyroscopique,
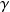, est donné par :
| (2.14) |
On suppose que les excitations extérieures sont aléatoires, stationnaires, indépendantes (décorrelées), et de densités spectrales constantes sur tout le spectre
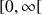(bruits blancs).
Cette configuration de couplage est à la base de la méthode SEA. Il a été démontré dans les années 60 que la moyenne temporelle de la puissance échangée de l'oscillateur 1 à l'oscillateur 2,
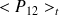, est proportionnelle à la différence des moyennes temporelles des énergies totales des oscillateurs
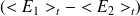(voir [LYO95]) :
| (2.15) |
où le coefficient d'échange énergétique
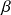est exprimé par :
| (2.16) |
La relation (2.15) montre que la puissance échangée va de l'oscillateur le plus énergétique vers le moins énergétique. On peut faire une analogie avec la thermique en considérant la loi de Fourier pour une paroi plane :
| (2.17) |
où :
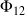est la densité de flux thermique surfacique de 1 vers 2,
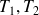sont les températures de part et d'autre de la paroi ;-
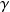est la conductivité thermique par unité d'épaisseur.
L'énergie joue le rôle de température et la constante d'échange énergétique
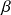joue le rôle de la conductivité thermique. En thermique, plus la conductivité thermique est grande, plus la paroi a une capacité à transmettre la chaleur entre les deux locaux (toujours du local le plus chaud vers le plus froid). Concernant la vibration des 2 oscillateurs, plus le coefficient d'échange énergétique est grand, plus les oscillateurs ont une capacité importante à échanger de l'énergie (toujours de l'oscillateur le plus énergétique vers le moins énergétique). On remarquera que le coefficient
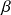dépend des pulsations propres des oscillateurs découplés, des constantes d'amortissement
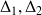et du coefficient de couplage
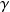. L'animation n°1 permet d'étudier la valeur de ce coefficient en fonction des pulsations propres des deux oscillateurs et de la constante d'amortissement (identique pour les 2 oscillateurs,
).
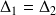Animation n°1 :
Cette relation établie pour deux oscillateurs n'est plus vraie dans le cas de trois oscillateurs. Elle constitue néanmoins une relation fondamentale pour la méthode SEA. En effet, lors de la 3ième partie de l'exposé, elle permettra sous hypothèses d'estimer la puissance échangée par deux modes à partir de leurs énergies modales.
Dans cette première partie, nous avons déterminé la puissance injectée et la puissance dissipée par un oscillateur ainsi que la puissance échangée par 2 oscillateurs couplés par un élément gyroscopique. Avant d'en arriver à la formulation proprement dite du modèle SEA, il faut établir le lien entre le comportement vibro-acoustique de deux systèmes continus couplés et le comportement d'un ensemble d'oscillateurs couplés entre eux.
