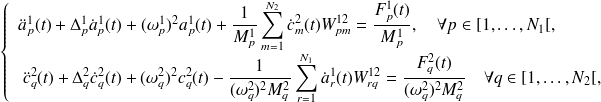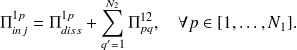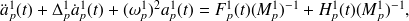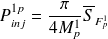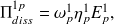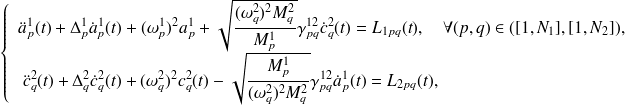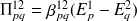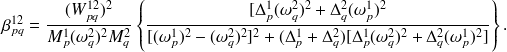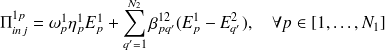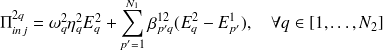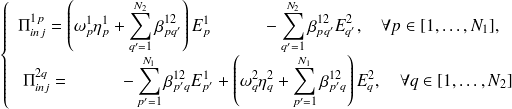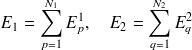Equations énergétiques modales du mouvement
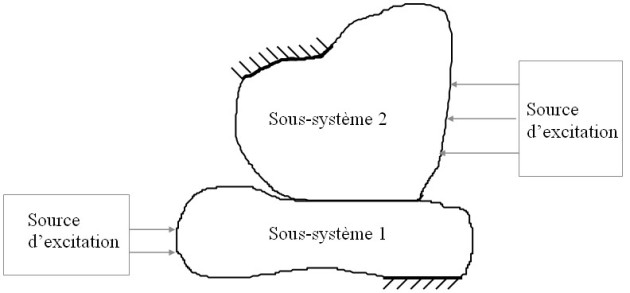
On considère maintenant deux sous-systèmes continus couplés et soumis à des excitations aléatoires, stationnaires, décorrelées et de type bruits blancs tronqués dans la bande de fréquence
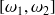 (typiquement, une bande tiers d'octave). On cherche à déterminer la réponse vibratoire dans la bande de fréquence
(typiquement, une bande tiers d'octave). On cherche à déterminer la réponse vibratoire dans la bande de fréquence
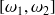 de ces sous-systèmes.
de ces sous-systèmes.
À partir des résultats de la double formulation modale donnée au paragraphe 3, on peut étudier l'interaction entre ces deux systèmes en considérant les couplages entre deux groupes de modes.
La méthode SEA suppose – hypothèse (H1) – que le comportement vibratoire dans la bande considérée peut être correctement analysé à partir de l'interaction entre les modes résonnants de la bande de fréquence (c'est-à-dire à partir des modes des sous-systèmes ayant leur fréquence propre contenue dans la bande de fréquence considérée). Différentes études numériques, on pu montrer que cette hypothèse était bien respectée si une rupture d'impédance était présente au niveau de la jonction entre les deux sous-systèmes et que les modes des sous-systèmes étaient bien choisis (i.e. sous-système le plus raide représenté par les modes libres et sous-système le plus souple représenté par les modes bloqués).
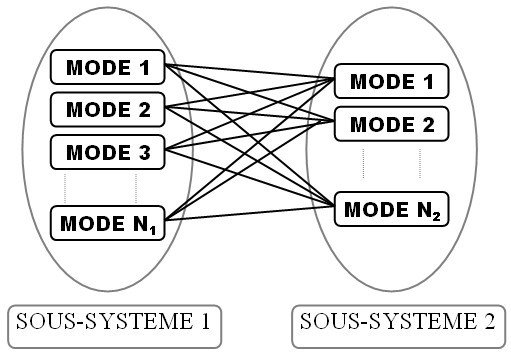
On considère donc l'interaction entre les
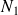 modes résonnants du sous-système 1 et les
modes résonnants du sous-système 1 et les
 modes résonnants du sous-système 2.
modes résonnants du sous-système 2.
Les équations respectées par les amplitudes de ces modes sont déduites des équations (3.6) du paragraphe 3 :
| (4.1) |
Compte tenu de la forme des équations modales (i.e. similitude des équations), ces modes peuvent être modélisés par des oscillateurs. Les couplages entre ceux-ci sont alors de type gyroscopique et peuvent se représenter par la figure 3.4. On rappelle que cette configuration ne fait pas intervenir de couplage direct entre les modes (oscillateurs) d'un même sous-système : un mode d'un sous-système est couplé avec les modes de l'autre sous-système mais n'est pas couplé avec les autres modes du sous-système auquel il appartient.
On cherche à calculer les énergies des modes en utilisant les relations de base établies au paragraphe 2. On rappelle que la relation d'échange de puissance entre deux oscillateurs est établie pour des oscillateurs excités par des bruits blancs sur la bande de fréquence
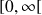 et que les énergies des oscillateurs sont définies en considérant cette même bande. Cependant, voir par exemple [MAI87], les transferts d'énergie entre les modes et les énergies totales de ceux-ci sont concentrés autour des fréquences de résonance. On peut donc raisonnable faire l'hypothèse que les énergies des modes résonnants correspondantes à la bande
et que les énergies des oscillateurs sont définies en considérant cette même bande. Cependant, voir par exemple [MAI87], les transferts d'énergie entre les modes et les énergies totales de ceux-ci sont concentrés autour des fréquences de résonance. On peut donc raisonnable faire l'hypothèse que les énergies des modes résonnants correspondantes à la bande
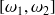 sont correctement approchées par les énergies de ces mêmes modes correspondantes à la bande
sont correctement approchées par les énergies de ces mêmes modes correspondantes à la bande
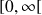 . Ceci est également valable pour les puissances échangées entre deux modes résonnants.
. Ceci est également valable pour les puissances échangées entre deux modes résonnants.
Pour ne pas alourdir l'écriture, on omettra à partir de maintenant de faire apparaître la moyenne temporelle sur les quantités énergétiques bien que celle-ci soit toujours considérée pour ces quantités.
Considérons un mode p du sous-système 1. On obtient l'équation qui traduit l'équilibre énergétique de ce mode en appliquant le principe de conservation de l'énergie pour un processus stationnaire :
| (4.3) |
Celle-ci exprime que la puissance injectée dans le mode p par l'excitation extérieure est, soit dissipée par l'amortissement interne du mode soit échangée avec les modes de l'autre sous-système. Nous allons évaluer chacun de ces trois termes à partir des relations établies sur les oscillateurs au paragraphe précédent :
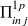 : Puissance injectée par la force généralisée due à l'excitation extérieure.
: Puissance injectée par la force généralisée due à l'excitation extérieure.
Les efforts appliqués sur ce mode sont dus à l'excitation extérieure de type bruit blanc et aux forces de couplage avec l'autre sous-système. En effet, si en (4.1), on isole le mode p, on a :
| (4.4) |
où
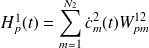 représente l'ensemble des efforts appliqués par les modes du sous-système 2 sur le mode p du sous-système 1.
représente l'ensemble des efforts appliqués par les modes du sous-système 2 sur le mode p du sous-système 1.
On suppose - hypothèse (H2) - que les forces de couplage,
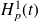 , sont telles que l'on puisse calculer
, sont telles que l'on puisse calculer
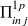 à partir de la relation (2.12) :
à partir de la relation (2.12) :
| (4.5) |
avec
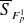 , la densité spectrale de la force généralisée
, la densité spectrale de la force généralisée
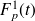 et exprimée en
et exprimée en
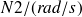 .
.
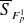 peut être calculée à partir de la déformée du mode p, et des données caractérisant la force extérieure appliquée au sous-système (densité spectrale, répartition spatiale).
peut être calculée à partir de la déformée du mode p, et des données caractérisant la force extérieure appliquée au sous-système (densité spectrale, répartition spatiale).
L'hypothèse (H2) posée plus haut peut être respectée dans plusieurs cas :
-les forces de couplage ont un effet négligeable sur le comportement du mode. Dans le cas d'une interaction faible entre les sous-systèmes, ceci est vérifié car le niveau de l'excitation extérieure est beaucoup plus élevé que celui de l'ensemble des forces de couplage en réaction ;
-l'ensemble des forces de couplage,
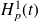 , constitue un processus décorrélé avec la force généralisée. Les modes sont alors excités par des excitations indépendantes les unes des autres, les puissances injectées peuvent être déterminées séparément. Ce cas peut se rencontrer quand plusieurs sous-systèmes sont excités par des excitations aléatoires réparties qui ne présentent pas de corrélations spatiales. On parle alors d'excitations ‘rain on the roof'.
, constitue un processus décorrélé avec la force généralisée. Les modes sont alors excités par des excitations indépendantes les unes des autres, les puissances injectées peuvent être déterminées séparément. Ce cas peut se rencontrer quand plusieurs sous-systèmes sont excités par des excitations aléatoires réparties qui ne présentent pas de corrélations spatiales. On parle alors d'excitations ‘rain on the roof'.
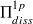 : Puissance dissipée par le mode p.
: Puissance dissipée par le mode p.
Compte tenu de l'hypothèse (H2) et de la relation (2.8) établie pour un oscillateur, on peut également écrire :
| (4.6) |
où
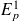 est l'énergie totale du mode p.
est l'énergie totale du mode p.
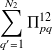 : Puissance échangée par le mode p avec les modes du sous-système 2.
: Puissance échangée par le mode p avec les modes du sous-système 2.
Pour évaluer la puissance échangée entre le mode p du sous-système 1 et le mode q du sous-système 2, on isole ces deux modes dans les équations modales du mouvement :
| (4.7) |
avec
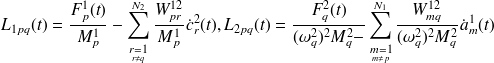 , et où on a fait apparaître
, et où on a fait apparaître
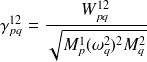 .
.
Par analogie avec les équations du mouvement des deux oscillateurs couplés (équation (3.13)), et en supposant - hypothèse (H3) - que
 et
et
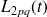 satisfassent les mêmes conditions que
satisfassent les mêmes conditions que
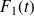 et
et
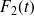 au paragraphe 2.2 (i.e. efforts décorrelés avec un spectre plat en fréquence), on peut écrire :
au paragraphe 2.2 (i.e. efforts décorrelés avec un spectre plat en fréquence), on peut écrire :
| (4.8) |
où
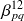 est appelé le facteur de couplage intermodal et peut être déterminé avec (2.16) en fonction des pulsations propres
est appelé le facteur de couplage intermodal et peut être déterminé avec (2.16) en fonction des pulsations propres
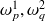 , des masses généralisées
, des masses généralisées
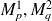 , des bandes d'amortissements modales
, des bandes d'amortissements modales
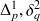 , et du travail d'interaction modale
, et du travail d'interaction modale
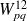 :
:
| (4.9) |
Le domaine de validité de l'hypothèse (H3) n'est pas facile à cerner. Elle implique 'une certaine indépendance' entre les amplitudes modales ce qui implique de nouveau une hypothèse de couplage faible entre les sous-systèmes. L'hypothèse (H3) trouve une légitimité plus forte à partir d'une moyenne d'ensemble sur une population de structures apparemment identiques. En effet, comme nous l'avons évoqué en introduction de cette présentation, en haute fréquence, des structures industrielles apparemment identiques peuvent présenter une forte dispersion de leurs caractéristiques vibratoires. Il apparaît donc illusoire de vouloir prédire la réponse d'une seule de ces structures. En considérant cette population de structures, les moyennes d'ensemble des efforts appliqués sur les modes p et q ont plus de « chance » de vérifier l'hypothèse (H3) que les efforts d'une seule structure de cette population.
Cette moyenne d'ensemble est à la base du caractère « statistique » de la méthode SEA. Alors que la dispersion vibratoire apparaît comme une faiblesse des méthodes déterministes (car elles ne peuvent la prévoir), la méthode SEA en fait une force en simplifiant la relation d'échanges énergétiques entre 2 modes (en utilisant la relation (2.15)). Néanmoins, en pratique, on ne connaît que très peu les caractéristiques de dispersion des structures que l'on considère. On ne peut donc pas dire si elle est suffisante pour que l'hypothèse (H3) puisse être raisonnablement respectée. Nous ne rentrerons pas plus dans le détail de ce point qui reste un sujet de recherche d'actualité.
Afin de mieux appréhender l'interaction énergétique des modes de deux sous-systèmes, on propose l'animation n°2 avec laquelle on peut étudier les valeurs des facteurs de couplage intermodaux
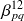 concernant deux poutres vibrant en flexion et couplées rigidement. La première poutre a une longueur de 2 mètres et a une épaisseur 2 fois plus fine que la 2ième poutre. On peut faire varier la longueur de la 2ième poutre ainsi que le facteur d'amortissement modal
concernant deux poutres vibrant en flexion et couplées rigidement. La première poutre a une longueur de 2 mètres et a une épaisseur 2 fois plus fine que la 2ième poutre. On peut faire varier la longueur de la 2ième poutre ainsi que le facteur d'amortissement modal
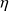 (avec
(avec
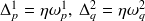 dans (4.9)). On remarquera l'évolution des facteurs en fonction de la différence des fréquences propres des 2 sous-systèmes ainsi que l'effet de l'amortissement. Plus l'amortissement est faible, plus les modes proches fréquentiellement (i.e. modes avec des fréquences propres voisines) ont des facteurs qui grimpent (ce qui traduit une forte capacité de ces modes à échanger de l'énergie), et à l'inverse les modes bien distincts fréquentiellement ont des facteurs qui chutent. Pour des amortissements très faibles, seul quelques couples de modes présentent une forte interaction. Les autres interactions sont négligeables. A contrario, quand l'amortissement augmente, les modes proches fréquentiellement ont des facteurs qui chutent et les modes bien distincts fréquentiellement ont des facteurs qui augmentent. Ceci a alors tendance à niveler les valeurs des facteurs de couplage intermodaux. Les modes d'un sous-système sont alors plus ou moins couplés avec la même intensité avec les modes de l'autre sous-système. On remarquera que ceci n'est pas valable dans tous les cas, notamment les cas où le couplage spatiale entre les modes joue un rôle prépondérant (influence du travail d'interaction modal,
dans (4.9)). On remarquera l'évolution des facteurs en fonction de la différence des fréquences propres des 2 sous-systèmes ainsi que l'effet de l'amortissement. Plus l'amortissement est faible, plus les modes proches fréquentiellement (i.e. modes avec des fréquences propres voisines) ont des facteurs qui grimpent (ce qui traduit une forte capacité de ces modes à échanger de l'énergie), et à l'inverse les modes bien distincts fréquentiellement ont des facteurs qui chutent. Pour des amortissements très faibles, seul quelques couples de modes présentent une forte interaction. Les autres interactions sont négligeables. A contrario, quand l'amortissement augmente, les modes proches fréquentiellement ont des facteurs qui chutent et les modes bien distincts fréquentiellement ont des facteurs qui augmentent. Ceci a alors tendance à niveler les valeurs des facteurs de couplage intermodaux. Les modes d'un sous-système sont alors plus ou moins couplés avec la même intensité avec les modes de l'autre sous-système. On remarquera que ceci n'est pas valable dans tous les cas, notamment les cas où le couplage spatiale entre les modes joue un rôle prépondérant (influence du travail d'interaction modal,
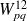 ). Pour le couplage de deux poutres à une extrémité, le couplage spatial des modes a peu d'influence
). Pour le couplage de deux poutres à une extrémité, le couplage spatial des modes a peu d'influence
Animation n°2
Revenons au bilan énergétique de chaque mode. En injectant (4.6) et (4.8) dans (4.3), on obtient une équation pour chaque indice p dont les inconnues sont les énergies des modes :
| (4.10) |
De la même manière, on écrit l'équilibre énergétique de chaque mode du sous-système 2 :
| (4.11) |
Les relations (4.10) et (4.11) forment un système d'équations linéaires à N1+N2 équations et N1+N2 inconnues :
| (4.12) |
Ces équations constituent ce que l'on appelle les équations énergétiques modales du mouvement et les inconnues sont les énergies modales des deux sous-systèmes. Les puissances modales injectées,
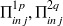 sont des données d'entrée et peuvent être évaluées à partir de (4.5). Celles-ci peuvent être différentes d'un mode à l'autre ; le modèle peut donc prendre en compte des excitations plus localisées que l'excitation ‘rain on the roof' tant que l'hypothèse (H2) reste vérifiée.
sont des données d'entrée et peuvent être évaluées à partir de (4.5). Celles-ci peuvent être différentes d'un mode à l'autre ; le modèle peut donc prendre en compte des excitations plus localisées que l'excitation ‘rain on the roof' tant que l'hypothèse (H2) reste vérifiée.
La résolution de ce système d'équations permet de déterminer la réponse vibratoire des sous-systèmes couplés en termes d'énergies modales. Les énergies totales des sous-systèmes peuvent ensuite être obtenues par sommation des énergies modales (de part la propriété d'orthogonalité des modes) :
| (4.13) |
où E1 (resp. E2) est la moyenne temporelle de l'énergie totale du sous-système 1 (resp. sous-système 2) correspondant à la bande de fréquence
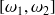 .
.
Ce modèle basé sur les équations énergétiques modales est appelé le modèle SmEdA (Statistical modal Energy distribution Analysis) [MAX03]. Il présente un domaine de validité plus étendu que le modèle SEA puisqu'une 4ième hypothèse (i.e. équirépartition des énergies modales) n'a pas encore été introduite.
Les équations énergétiques modales ont été obtenues pour deux sous-systèmes couplés. Elles peuvent être aisément déduites pour un nombre quelconque de sous-systèmes.