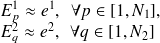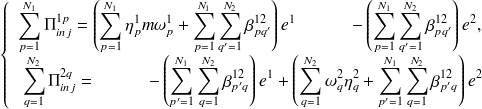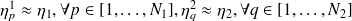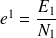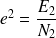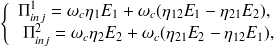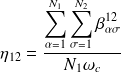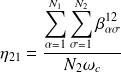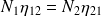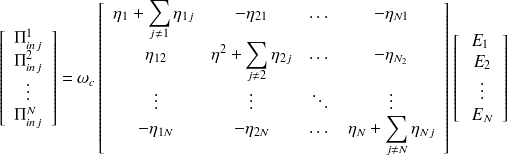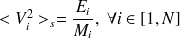Equations SEA
Pour des structures complexes composées de multiples sous-systèmes, le nombre de modes à prendre en compte dans les équations énergétiques modales peut devenir important. La méthode SEA fait alors l'hypothèse (H4) d'équirépartition des énergies modales, c'est-à-dire qu'elle suppose que les modes d'un même sous-système répondent globalement de la même façon et donc qu'ils présentent les mêmes niveaux d'énergies :
| (4.14) |
Cette hypothèse n'est pas bien respectée quand les sous-systèmes présentent peu de modes résonnants, quand les sous-systèmes sont très hétérogènes (ce qui induit des modes localisés à l'intérieur du sous-système) ou encore quand les excitations extérieures sont localisées spatialement (certains modes sont alors plus excités que d'autres). Dans ces cas, on privilégiera les équations SmEdA.
En introduisant cette hypothèse (H4) dans le système d'équations formé par (4.10) et (4.11), et en sommant les équations relatives à chaque sous-système, on obtient le système de 2 équations à 2 inconnues :
| (4.15) |
En lien avec l'hypothèse d'équirépartition des énergies modales, on suppose que les facteurs d'amortissements modaux d'un même sous-système sont en approximation identiques :
| (4.16) |
Compte tenu que la largeur de la bande de fréquence
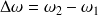est petite devant la fréquence centrale
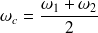, on peut considérer l'approximation :
| (4.17) |
Par ailleurs, à partir de l'équation (4.13), on peut déterminer les énergies modales moyennes
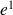et
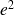à partir des énergies totales des sous-systèmes et des nombres de modes résonnants :
| (4.18) |
En introduisant ces expressions dans le système (4.15), on obtient les équations SEA :
| (4.19) |
où :
on a posé
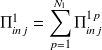et
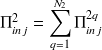, qui représentent les puissances injectées dans les sous-systèmes 1 et 2 par les excitations extérieures, et ;on a fait apparaître les facteurs de perte par couplage
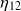et
:
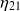| (4.20) |
Ces facteurs de perte par couplage sont définis par analogie avec les facteurs de perte interne. Ils traduisent la capacité des sous-systèmes à échanger de l'énergie entre eux. On peut remarquer qu'ils respectent une relation dite de réciprocité :
| (4.21) |
Les équations SEA (4.19) établies pour 2 sous-systèmes peuvent être facilement étendues à N sous-systèmes :
| (4.22) |
En résolvant le système (4.22), on obtient les énergies totales de chaque sous-système. Ces énergies caractérisent la réponse du système mais elles présentent l'inconvénient d'être difficilement interprétables en pratique. Pour relier cette quantité énergétique à une quantité physique plus facilement interprétable, on approxime l'énergie totale par le double de l'énergie cinétique (comme pour un oscillateur, voir Eq. (2.6)). Cette approximation se vérifie bien tant que l'on considère les énergies totales dues à la contribution des modes résonnants.
On peut alors écrire les vitesses quadratiques moyennées sur chaque sous-système à partir des énergies totales et des masses des sous-systèmes:
| (4.23) |
On rappelle que ces résultats concernent la bande de fréquence
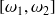(typiquement une bande de tiers d'octave). Le modèle SEA permet donc d'estimer des quantités vibratoires moyennées spatialement pour chaque sous-système et par bande de fréquence. Elle ne donne pas d'informations locales ou à des fréquences bien déterminées. Par contre, elle présente des temps de calcul très court et elle donne une vision d'ensemble du comportement du système (d'où le A, d'analyse dans le nom de la méthode). Les données d'entrée du système sont les puissances injectées par les sources extérieures, les facteurs de perte par couplage et les facteurs de perte interne. Ces derniers sont généralement estimés expérimentalement (en utilisant la méthode SEA inverse par exemple). La formulation de base de la SEA donne une façon de calculer les puissances injectées (voir Eq. (4.9)) et les facteurs de perte par couplage (voir Eq. (4.20) avec Eq. (4.5)) à partir de la connaissance des modes propres de chaque sous-système. De nombreuses approches alternatives ou complémentaires ont été développées, notamment pour les sous-systèmes présentant une forte densité de modes. On rappelle que différentes hypothèses (H1) à (H4), ont été posées pour aboutir aux équations SEA. Ces hypothèses ne sont pas faciles à appréhender et à vérifier en pratique. On peut donner quelques indications pratiques à respecter :
les excitations doivent être aléatoires, large bande en fréquence et décorrelées (vis-à-vis de (H2) et (H3)) ;
les sous-systèmes doivent présenter un nombre suffisant de modes par bande de fréquence (vis-à-vis de (H4)) ;
l'amortissement des sous-systèmes ne doit être ni trop faible (H4 non vérifiée), ni trop fort (H3 non vérifiée) ;
le couplage entre les sous-systèmes doit être faible (vis-à-vis de (H1) à (H4)). La manière de décomposer le problème global en différents sous-systèmes (sous-structuration SEA) est donc très important pour le respect de cette hypothèse de couplage faible. La sous-structuration doit faire apparaître des ruptures d'impédances mécaniques au niveau des jonctions de couplage entre les sous-systèmes (différence de raideurs de part et d'autre de la jonction). Pour plus de détails sur sujet, on pourra consulter [TOT06].
