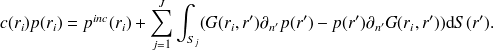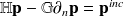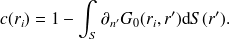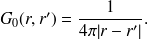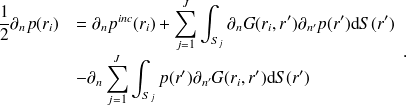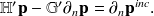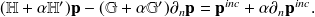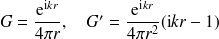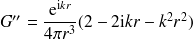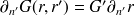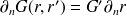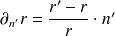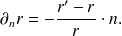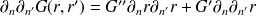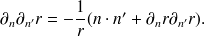Méthode de collocation
La méthode de collocation consiste à appliquer l'équation (9) en un ensemble de
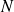points
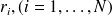localisés sur la surface de la structure. Cela donne
| (28) |
On choisit de préférence (mais ce n'est obligatoire) les points de collocation de telle manière qu'ils coincident avec les noeuds des éléments et, après intégration on aboutit à un système linéaire liant le vecteur
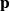contenant la pression aux noeuds au vecteur
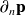contenant la dérivée normale :
| (29) |
La résolution du système (29) nécessite de connaitre les conditions aux limites sur la surface (en général : pression, vitesse ou une relation d'impédance). Par exemple, le champ diffracté par une structure rigide s'obtient simplement en inversant la matrice
. La pression peut être ensuite retrouvée en tout point en appliquant (9) pour un point
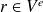. Si la surface n'est pas régulière au voisinage du point de collocation (point anguleux, arête..), il faut calculer le coefficient géométrique. Une astuce consiste à considérer l'équation pour le champ interne (15) à la fréquence nulle. Dans ce cas la solution constante est solution du problème, par conséquent
| (30) |
Ici,
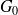est la fonction de Green de l'équation de Laplace :
| (31) |
Le système d'équation (29) peut être considéré comme la version ‘simple' de la méthode des éléments de frontière pour les problèmes de propagation acoustique en milieu extérieurs. Rappelons que lorsque la fréquence augmente, la présence des résonances internes peut s'avérer génant d'un point de vue numérique (voir Section 3) et cela est suffisant pour rendre la méthode inutilisable ! La méthode de Schenk, bien que plus simple à implémenter est moins stable et moins précise que celle de Burton & Miller. Pour utiliser cette dernière il faut s'assurer que la surface soit régulière au point de collocation, puis de combiner (28) avec
| (32) |
Ce qu'on peut écrire sous forme matricielle
| (33) |
La système combiné devient
| (34) |
|---|
Remarque : Remarques sur les procédures d'intégration
Pour le calcul de ces intégrales, rappelons que (on note
) :
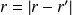| (35) |
où le symbole (′) désigne la dérivée selon
. Ainsi, les dérivées normales s'écrivent
| (36) |
avec
| (37) |
Le dérivée seconde est plus délicate :
| (38) |
avec
| (39) |
Lorsque le point de collocation
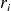n'appartient pas à l'élément à intégrer
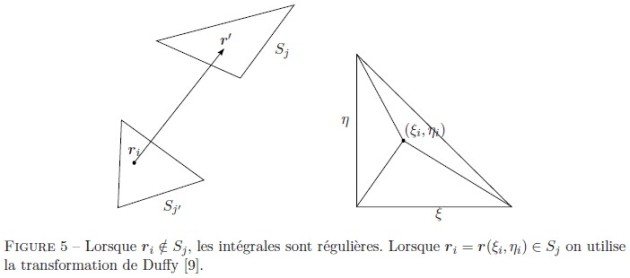
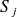(les bords inclus !), les intégrales sont toutes régulières et on peut appliquer les méthodes d'intégrations de Gauss- Legendre. Si le point appartient à la surface à intégrer, les intégrales faisant intervenir la fonction de Green et ses dérivées premières sont intégrables au sens classique. Numériquement il faut utiliser des techniques d'intégration adaptées pour que le comportement singulier soit bien pris en compte dans le calcul. Une technique efficace est d'utiliser la transformation non-linéaire de Duffy [9] dans l'espace de référence
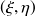(voir figure 5). Cela consiste à partitionner l'élément de référence (en général, triangulaire ou carré) en sous-domaines triangulaires avec pour sommet commun le point singulier
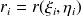. La méthode consiste à se débarrasser de la singularité grâce au Jacobien de la transformation. L'intégrale faisant intervenir la dérivée seconde de G est hyper-singulière et n'est pas intégrable au sens classique. Pour contourner la difficulté, des techniques de régularisation existent [7, 8].
