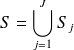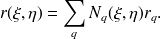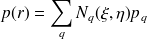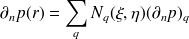Introduction
Pour illustrer la méthode, nous reprenons le problème de diffraction décrit par l'équation (9). La première étape est de procéder à une discretisation de la surface
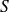: on pose que
|
où chaque élément de surface
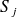admet une paramétrisation régulière. Classiquement, on prend des fonctions de forme inspirées de la méthode des éléments finis :
| (26) |
Ici,
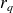sont des noeuds géométriques et
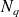les fonctions de forme classique (linéaire, quadratique, etc...). La deuxième étape est d'approximer le champ de pression et de vitesse sur chaque élément. Le choix de l'approximation dépend en partie de l'équation intégrale à discrétiser, de la méthode de résolution : méthode de collocation et variationnelle et enfin du comportement de la solution au voisinage de singularités géométriques (coins, arêtes...) ou de discontinuité sur les conditions aux limites (saut d'impédance par exemple). Ici encore, on choisit en général de prendre une approximation de type éléments finis pour les champs de pression et de vitesse :
| (27) |
où
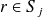est donné par (26) et les coefficients
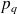correspondent à la valeur de la pression au noeud
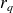(idem pour
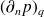). Notons que les deux approximations (26) et (27) sont identiques dans le cas d'éléments isoparamétriques mais d'autres options sont possibles, on peut utiliser des éléments sub-paramétriques ou super-paramétriques par exemple.
