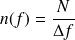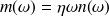Applications pratiques de la SEA

La densité modale des sous-systèmes n'est pas directement nécessaire à l'application des équations de la SEA. Toutefois, comme cela a été vu dans le cours « Formulation de base du modèle SEA » cette grandeur intervient directement dans les hypothèses de la SEA (ie : pour que l'hypothèse H4 soit respectée il faut que les sous-systèmes présentent un nombre suffisant de modes par bande de fréquence). Ainsi, pour savoir si les hypothèses sont respectées il est nécessaire d'avoir une estimation de la densité modale.

La densité modale représente le nombre de modes compris dans une bande de fréquence. On peut donc exprimer la densité modale :

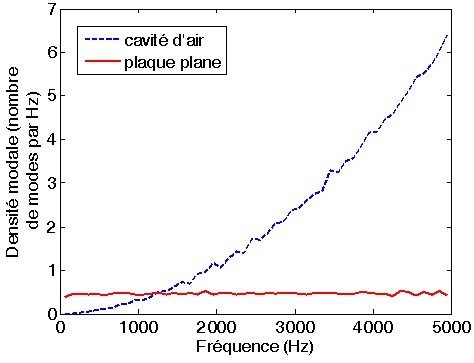
où N est le nombre de modes résonants dans la bande de fréquence 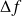. La densité modale dépend donc de la fréquence. Toutefois dans le cas d'une plaque, cette densité est pratiquement constante avec la fréquence alors qu'elle a une évolution exponentielle dans le cas d'une cavité d'air avec parois rigides comme cela est montré en figure 2.3.

Figure 2.3. Densité modale d'une plaque plane rectangulaire appuyée (trait plein) et d'une cavité d'air à parois rigides (pointillés).

Estimer la densité modale d'un sous-système permet d'obtenir un paramètre crucial dans l'évaluation du domaine de validité de la SEA : le recouvrement modal.

Le recouvrement modal se définit comme

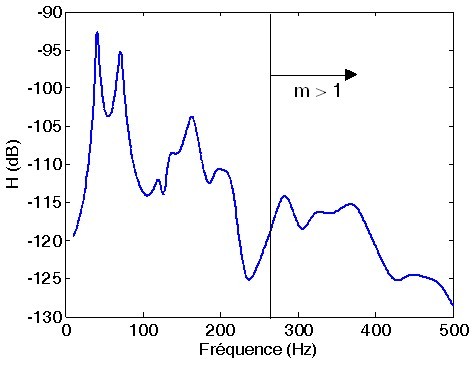
Le recouvrement modal permet de déterminer si le comportement du sous-système est dominé par ses modes (recouvrement modal inférieur à 1). Il est démontré, notamment en [LEB10], qu'un recouvrement modal supérieur à 1 est un critère nécessaire à l'application de la SEA (ce qui permet de respecter l'hypothèse d'équi-partition des énergies modales, hypothèse H4). La figure 2.4 montre une réponse d'une plaque et indique la fréquence à partir de laquelle le recouvrement modal est supérieur à 1.

Figure 2.4. Réponse d'un sous-système à fort recouvrement modal. Le recouvrement modal est supérieur à 1 à droite de la ligne verticale.