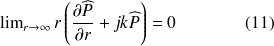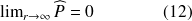Formulation intégrale des problèmes d'acoustique

On se place dans un premier temps dans le cadre d'un espace infini, sans aucun obstacle (nous verrons plus loin comment les prendre en compte). On cherche la pression rayonnée par un ensemble de sources localisées dans un volume fini. On cherche donc à déterminer la pression vérifiant :

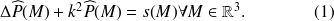
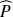représente indifféremment la transformée de Fourier de la pression acoustique ou son amplitude complexe en régime harmonique permanent.

Étant donné qu'on se place en espace infini, il n'y a pas de condition limite autre que celle traduisant que le champ de pression est tel qu'il n'y a pas de réflexion à l'infini. La traduction mathématique de cette condition sera abordée plus loin. La formulation intégrale de base est issue de l'application du théorème d'Ostogradski, en utilisant un domaine fluide constitué du volume compris entre deux sphères de rayon a et A, centrées en un point choisi arbitrairement et noté 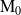. Ce domaine, noté 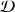, est grisé sur la figure 1 : les deux sphères sont choisies de telle façon qu'elles contiennent l'ensemble des sources.

Fig 01 - Illustration bidimensionnelle du domaine d'intégration

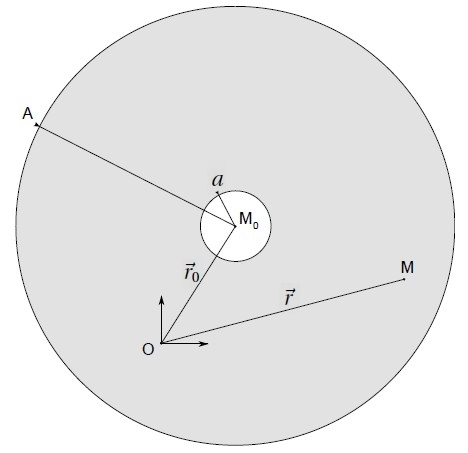
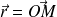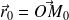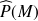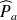On note et . L'objectif est de calculer la pression , et pour cela on va utiliser la solution d'un problème de référence, qui est le champ de pression rayonné par la sphère pulsante de rayon . Ce champ est noté et son expression est :

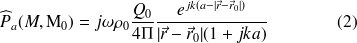
D'après l'équation (1), il est clair que :

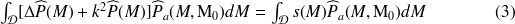
L'utilisation du théorème d'Ostogradski permet d'écrire le premier membre sous la forme :

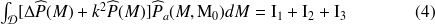
avec :

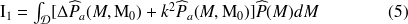
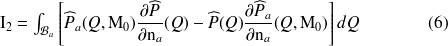
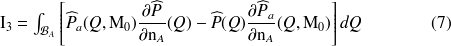
où 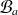(resp. 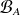) désigne la surface de la sphère de rayon (resp. A), et l'orientation des normales indique le sens de dérivation : 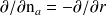et

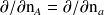
Nous pouvons alors évaluer chaque intégrale de l'expression précédente :

• Le calcul de la première intégrale est immédiat, puisque 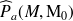est une solution de l'équation d'Helmholtz homogène : .

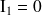• L'intégrale 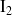va être calculée en faisant tendre le rayon vers 0, ce qui fait tendre le point Q (situé sur la surface 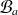) vers le point :

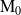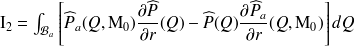
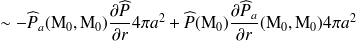
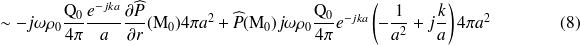
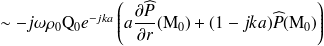
Il est alors clair que :

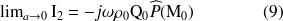
• L'intégrale 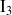va être calculée en faisant tendre le rayon A vers l'infini :

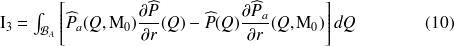
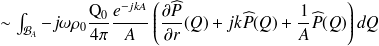
S'il n'y a pas de source à l'infini, la contribution de cette intégrale doit être nulle, ce qui traduit physiquement l'impossibilité d'une réflexion d'onde. L'élément d'intégration 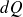étant homogène à 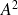, on peut en déduire les deux relations suivantes :

Ces deux relations sont appelées conditions de rayonnement et de finitude de Sommerfeld.

Finalement, la somme des trois intégrales conduit à l'expression suivante :

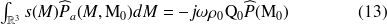
Soit, en choisissant le monopôle utilisé arbitrairement de telle façon que 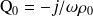et en notant sa pression 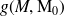, on a :

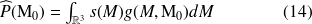
avec :

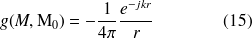
La fonction g est appelée fonction de Green en espace infini. Le champ généré par les sources 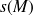peut donc être vu comme un cumul de champs rayonnés par des sources monopolaires d'amplitude .
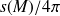