Fonction de Green
La formulation présentée a été développée en utilisant une fonction esclave arbitraire lors de l'intégration initiale, qui est la fonction de Green en espace infini. Mathématiquement, cette fonction peut être interprétée au sens des distributions comme étant la solution du problème acoustique suivant :
où
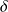est la distribution de Dirac. g est donc la solution du problème acoustique lorsque
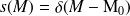, lorsqu'aucun obstacle n'existe dans
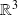. On peut en fait définir la fonction de Green de façon différente, en choisissant par exemple une fonction plus adaptée aux conditions réelles. Par exemple, pour le cas précédent qui comportait un obstacle rigide, on peut choisir d'utiliser une fonction de Green
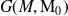qui est définie par :
Dans ce cas, l'intégrale portant sur S est nulle puisque la dérivée normale de la pression et de la fonction de Green sont toutes deux nulles. On obtient donc :
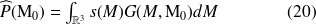
L'expression de la pression est donc à nouveau explicite. Par contre, la forme simple de g ne permet pas de vérifier les conditions sur S : la détermination de la fonction de Green G nécessite un calcul qui peut être complexe en fonction de la forme de l'obstacle.
On pourra donc toujours utiliser une fonction de Green G solution de
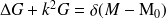, en lui adjoignant des conditions limites arbitraires, et on obtiendra toujours la même forme de solution :
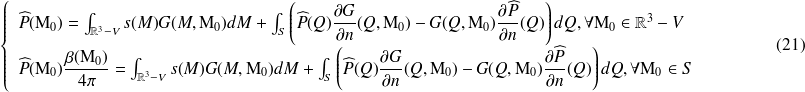
Suivant la définition adoptée pour la fonction G, la formulation sera explicite ou implicite : plus les conditions utilisées pour définir la fonction de Green sont proches des conditions réelles, plus la formulation intégrale est simple, mais plus la détermination de G est compliquée.
