Cas de l'espace fini
Dans le cas où l'on s'intéresse à la résolution du problème acoustique en espace clos, la formulation intégrale est identique. En notant V le volume dans lequel on cherche la solution, et S la surface qui clôt ce volume (constituées de parois rigides, vibrantes et/ou absorbantes), on a :
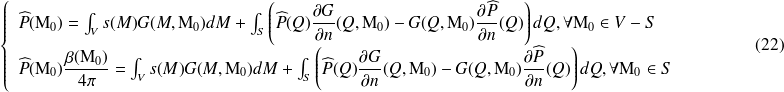
La fonction de Green G peut être la fonction de Green en espace infini g , ou toute autre fonction de Green construite avec des conditions limites arbitraires. Dans le cas de l'espace clos, le milieu possède des modes, et si l'on ne modélise pas de phénomène dissipatif, la solution
n'est pas définie lorsque la fréquence d'excitation est égale à une fréquence propre. Mathématiquement, cela se traduit par une intégrale sur S qui est non définie. Or, si l'on observe la formulation intégrale en espace infini avec un obstacle qui a la même forme que l'espace clos précédent, on s'aperçoit que cette intégrale y figure également. Ainsi, la formulation intégrale en milieu infini avec obstacle ne permettra pas de déterminer la pression lorsque la fréquence sera égale à une fréquence propre du domaine correspondant au volume de l'obstacle. Ces fréquences sont appelées fréquences singulières et peuvent poser problème lors de l'implémentation numérique de la formulation intégrale.
