Formulation intégrale en espace infini avec obstacle
La présence d'un obstacle dans l'espace ne change pas fondamentalement la technique présentée précédemment. La figure 2 présente le nouveau problème, similaire au précédent excepté qu'un obstacle rigide de volume V fermé par une surface S est présent dans l'espace.
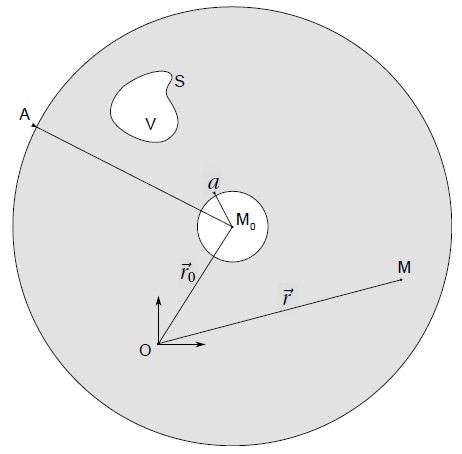
La méthodologie précédente conduit immédiatement, en utilisant la même fonction de Green, à :
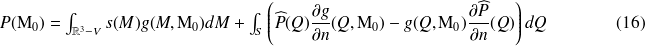
On peut donc voir la contribution de l'obstacle au champ de pression comme le cumul d'un ensemble de monopôles et de dipôles répartis sur la surface S :
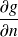peut être associé à un dipôle,
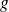peut être associé à un monopôle.
Si l'obstacle est vibrant,
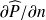est directement relié à la vitesse de vibration, qui peut être connue ou non, tandis que si l'obstacle est rigide, ce terme est nul. Cette équation présente cependant un inconvénient : elle est implicite, puisque
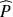apparaît dans l'intégrande, ce qui doit être pris en compte avec attention lors d'une implémentation numérique. Pour déterminer la pression en un point donné de l'espace, il faut donc connaître la pression sur l'obstacle. Il est important de noter que l'expression (16) n'est pas valable si
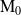est sur l'obstacle, car l'intégrale
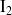ne converge plus vers la valeur
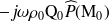puisque la surface d'intégration n'est plus une sphère complète mais uniquement une portion de sphère. Si on note
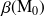l'angle solide associé au point
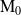, on a :
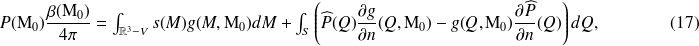
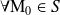
En particulier, si le point
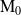est régulier (non anguleux), on a
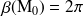, ce qui permet de montrer que pour un point régulier, la pression sur l'obstacle est deux fois plus importante que la pression au voisinage de l'obstacle.
