Cas de l'espace semi-infini : les sources images
On considère à présent le cas où l'on cherche à résoudre l'équation d'Helmholtz en espace semi-infini : le demi-espace considéré (noté
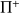) est délimité par un plan rigide noté
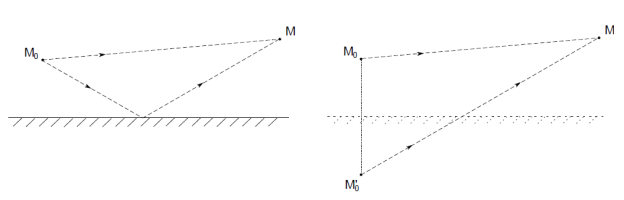
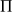. Le problème est illustré sur la partie gauche de la figure 3. Les sources sont notées
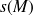et la condition de réflexion sur le plan s'écrit
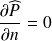sur
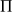. En utilisant une fonction de Green
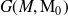construite avec des conditions limites identiques au problème de référence (s'il n'y a pas d'obstacle, c'est la fonction de Green en espace infini g ), on a :
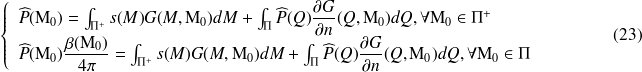
L'idée est alors de choisir une fonction de Green qui annule la contribution de l'intégrale sur
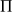, c'est-à-dire qui soit telle que
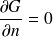sur
. Il suffit pour cela d'utiliser la fonction de Green
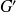suivante :
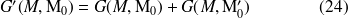
où
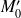est le symétrique de
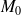par rapport au plan
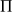. On obtient alors une formulation explicite :
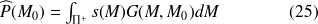
Cette équation est alors valable dans
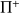mais également sur le plan
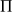qui n'est plus considéré dans cette formulation : le calcul se fait sur l'espace complet en considérant les sources et leurs images par rapport au plan
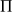, comme illustré sur la figure 3.
