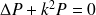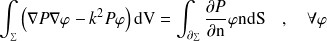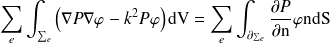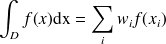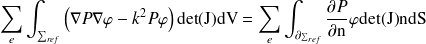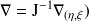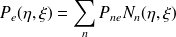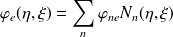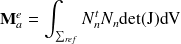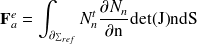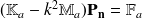2 Éléments finis pour l'acoustique
Les phénomènes relatifs à la propagation acoustique dans un milieu fluide sans écoulement et en régime harmonique
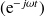sont décris par l'équation d'Helmholtz :
| (1) |
où
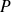est la pression et
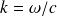le nombre d'onde.
La formulation faible associée est obtenue en mulitpliant par une fonction test
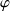et en intégrant par parties :
| (2) |
La normale unitaire n est choisie sortante au domaine. Le terme de gauche correspond au terme de domaine, et le terme de droite correspond au terme de bord utilisé pour coupler le domaine fluide à un autre domaine, ou pour imposer des conditions limites.
Le domaine est ensuite discrétisé en élements :
| (3) |
Les intégrales sont évaluées à l'aide d'une intégration par points de Gauss :
| (4) |
Elles ne sont cependant pas calculées directement dans le repère global mais à partir d'un élément de référence et d'une transformation géométrique. Le Jacobien J de la transformation permet alors de revenir à l'élément réel :
| (5) |
L'opérateur différentiel
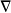dans le repère global se calcule dans le repère de référence avec la transformation suivante :
| (6) |
La pression et la fonction test peuvent maintenant être interpolées par des fonctions polynomiales sur chaque élément de référence
:
| (7) |
| (8) |
avec
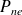l'inconnue du noeud
de l'élément de référence e correspondant, et
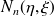la fonction de forme polynomiale définit comme étant non nulle au noeud
et nulle sur les autres noeuds.
Au final, nous arrivons au système :
| (9) |
où les matrices élémentaires de raideur, de masse et d'efforts apparaissent sous la forme :
| (10) |
| (11) |
| (12) |
L'assemblage des matrices élémentaires amène ensuite aux matrices globales de masse, raideur et d'effort, respectivement
,
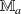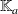, et
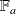. Le système (9) se réduit alors en :
| (13) |
Le terme de bord à droite est soit utilisé pour imposer des conditions limites, soit utilisé pour le couplage avec un autre domaine.
