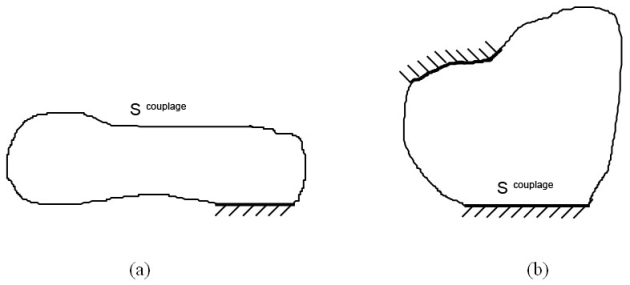
Modes des sous-systèmes découplés
Pour définir les modes des sous-systèmes découplés, il faut définir des conditions aux limites appropriées au niveau de la jonction de couplage
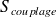pour chacun des sous-systèmes.
Deux types de conditions aux limites à la jonction sont considérées dans la double formulation modale : les conditions « encastrement » correspondant à des déplacements nuls et les conditions « libre » correspondant à des contraintes nulles.
Ces conditions aux limites donnent lieu à deux types de modes :
les modes avec des conditions « encastrement » à la jonction de couplage sont appelés les modes du sous-système découplé-bloqué ou plus simplement les modes bloqués ;
les modes avec des conditions « libre » à la jonction de couplage sont appelés les modes du sous-système découplé-libre ou plus simplement les modes libres.
D'un point de vue de la modélisation SEA, on verra qu'il est nécessaire qu'un couplage « faible » soit effectif entre les deux sous-systèmes, c'est-à-dire qu'il faut notamment que les impédances mécaniques des deux sous-systèmes soient très différentes au niveau de
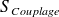(c'est ce que l'on a imposé au début de ce paragraphe). Le choix des modes (bloqués ou libres) pour chaque sous-système devient alors naturel sous cette condition. Ceci se retrouve dans la définition de Fahy du couplage faible [FAH96], « Sous des conditions de couplage faible, les modes du système sont ‘localisés' dans le sens qu'ils ressemblent de près en fréquences propres et en déformés aux modes des sous-systèmes découplés (avec les conditions aux limites appropriées)... »
. On en déduit que les modes des sous-systèmes découplés doivent être choisis tels qu'ils ressemblent aux modes physiques de la structure globale. Dans le cas du couplage faible, il y a une rupture d'impédance entre les deux sous-systèmes qui conduit à ce qu'un sous-système vibre plutôt librement alors que l'autre vibre plutôt comme s'il était encastré au niveau de la jonction entre les 2 sous-systèmes. Les modes libres sont alors les modes physiques du sous-système qui vibre plutôt librement et les modes bloqués sont les modes physiques de l'autre sous-système qui a tendance à être bloqué par le premier sous-système. Pour notre cas, le sous-système 1 (i.e. le plus raide) doit donc être décrit par les modes découplés-libres alors que le sous-système 2 doit être décrit par les modes découplés-bloqués (voir figure 3.2).
La double formulation modale impose alors de décrire en déplacement le sous-système représenté par ses modes libres et en contrainte le sous-système représenté par ses modes bloqués. Par conséquent, les déformées propres des modes doivent être caractérisées par ces variables (i.e. déplacements pour le sous-système 1, contraintes pour le sous-système 2).
On définit les schémas modaux :
pour le sous-système 1 découplé-libre :
pour le sous-système 2 découplé-bloqué :
