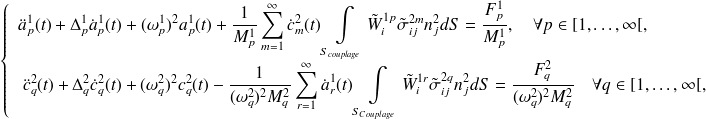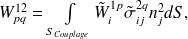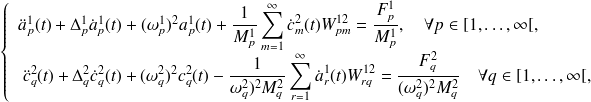Vibrations forcées des sous-systèmes couplés
En introduisant les termes d'excitation et d'amortissements visqueux dans (3.3), on obtient un système d'équations décrivant la réponse forcée des sous-systèmes couplés à partir des amplitudes modales des modes des sous-systèmes découplés :
| (3.4) |
où on a introduit des amortissements modaux de type visqueux par les bandes d'amortissement modales
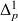et
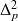, et les excitations extérieures par des forces généralisées.
Compte tenu de sa forme, ce système d'équations (3.4) peut être interprété comme le couplage d'un ensemble d'oscillateurs (modes) associés au sous-système 1 avec un autre ensemble d'oscillateurs associés au sous-système 2. On remarque qu'il n'y a pas de ‘couplages directs' entre les modes d'un même sous-système contrairement à ce que l'on aurait obtenu à partir d'une formulation en déplacement (voir [CRA71]). En effet, on constate que le mode p du sous-système 1 est couplé avec les modes du sous-système 2 mais il n'est pas couplé directement avec les autres modes du sous-système 1. Ceci est une conséquence de la double formulation contrainte-déplacement utilisée pour obtenir ces équations. Ce schéma de couplage modal est à la base de la formulation du modèle SEA.
En posant pour chaque couple de modes (p,q) :
| (3.5) |
le système d'équations peut se réécrire :
| (3.6) |
Du point de vue physique, on remarque que le terme
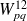, produit d'un effort et d'un déplacement, représente un travail échangé par le pième mode libre du sous-système 1 et le qième mode bloqué du sous-système 2. On appelle donc ce terme le travail d'interaction modale.
Les relations écrites dans ce paragraphe font intervenir des séries comportant une infinité de termes, c'est-à-dire qu'elles considèrent une infinité de modes. Ces séries sont convergentes (voir [KAR66]) et permettent de décrire les champs de déplacement et de contrainte des sous-systèmes couplés à partir de (3.1-3.2). Dans la formulation SEA, nous verrons qu'uniquement les modes résonnants dans la bande de fréquence considérée seront pris en compte, ce qui conduira à approximer les différents champs. Cette approximation sera suffisante sous une condition de couplage faible.
