Introduction
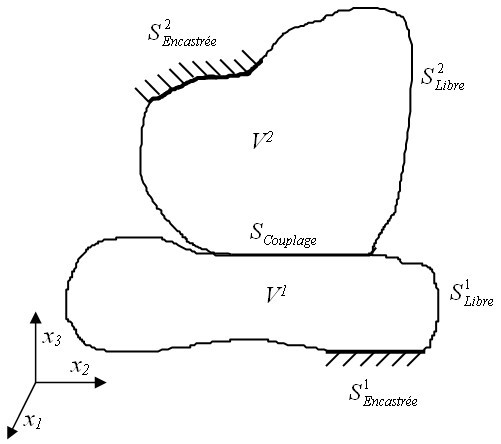
On considère un système mécanique, continu, tridimensionnel, déformable au sens de la théorie de l'élastique, et composé de deux sous-systèmes couplés rigidement sur une surface
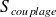comme représenté figure 3.1. La sous-structuration du système est définie telle qu'il y ait une rupture d'impédance mécanique au niveau de la jonction de couplage, c'est-à-dire que l'un des sous-systèmes est plus raide que l'autre vue de cette jonction. On supposera que le sous-système 1 est plus raide, et donc que le sous-système 2 est plus souple. On s'intéresse dans un premier temps aux vibrations libres du système (c'est-à-dire sans considérer d'excitation extérieure). On note
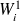et
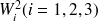, les déplacements (dans les 3 directions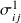) et
et
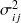, les tenseurs de contraintes en chaque point des sous-systèmes 1 et 2, respectivement.
La double formulation modale permet de décrire le comportement dynamique de ces deux sous-systèmes couplés sur la base de modes propres des sous-systèmes découplés. Cette formulation basée sur une double formulation contrainte-déplacement n'est pas classique pour les systèmes mécaniques couplés. Toutefois, la double formulation modale est une approche standard utilisée pour étudier le couplage entre une cavité acoustique et une structure mécanique. Nous ne détaillons pas ici les développements de cette formulation (qui peuvent être trouvés en [MAX01]) mais nous en donnons les principaux résultats.
