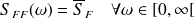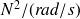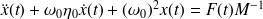Introduction
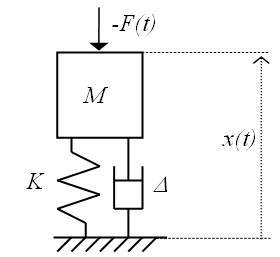
On considère un système 1 degré de liberté (i.e. oscillateur) composé d'une masse M, d'un ressort de raideur K et d'un amortisseur de constante
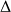(voir figure 2.1). L'amortissement du système est supposé de type visqueux, c'est-à-dire que la force exercée par l'amortisseur s'oppose au mouvement de la masse M et son intensité est proportionnelle à la vitesse de la masse M.
Ce système est soumis à une force aléatoire stationnaire
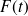de type bruit blanc, c'est-à-dire que la densité spectrale du signal
,
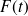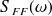est constante pour toutes les fréquences :
(exprimée en
| (2.1) |
L'équation du mouvement
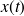de la masse M peut alors s'écrire sous la forme :
| (2.2) |
avec
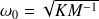: la fréquence propre en rad/s de l'oscillateur ;
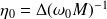: le facteur d'amortissement interne ou DLF (Damping Loss Factor).
On s'intéresse uniquement au régime stationnaire de l'oscillateur (c'est-à-dire que l'on néglige le régime transitoire).
