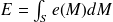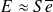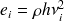Mesure
L'énergie cinétique d'une structure peut être mesurée à l'aide d'un capteur de vitesse (vibromètre laser) ou d'accélération (accéléromètre). Toutefois, l'estimation de l'énergie cinétique globale du sous-système nécessite un nombre de point de mesure très important, répartis sur toute la surface de la plaque. En effet, l'énergie globale du sous-système est reliée à la densité d'énergie (énergie par unité de surface) en un point M par la relation suivante :
| (2.5) |
La mesure de la densité d'énergie n'étant possible que sur un nombre finis
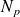de points de mesure, le calcul de l'intégrale doit être approximé par une sommation
| (2.5) |
où
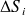est la surface élémentaire associée au point de mesure i sur lequel la densité d'énergie a été mesurée. Dans le cas d'un maillage de points régulièrement espacés sur la surface du sous-système, l'énergie cinétique globale devient
| (2.5) |
où S est la surface du sous-système et
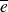est la densité d'énergie moyenne.
La densité d'énergie est mesurée, localement, grâce à la connaissance de la vitesse vibratoire du sous-système au point i
| (2.5) |
où
et h sont respectivement la masse volumique et l'épaisseur du sous-système au point i.
Il est évident que la qualité de l'estimation de l'énergie globale du sous-système dépend directement du nombre de points utilisés dans l'équation (2.5). Plus le maillage de points utilisé sera fin, meilleure sera l'estimation de l'énergie globale. De même, la longueur d'onde dans le sous-système diminuant avec la fréquence, le maillage de point de mesure devra être très fin à haute fréquence. Un critère de maillage basé sur la longueur d'onde dans le sous-système (comme celui utilisé en éléments finis) peut être choisi. Par exemple, on adaptera l'espacement entre les points de manière à ce qu'il respecte
où
est la longueur d'onde des ondes de flexion du sous-système. La longueur d'onde des ondes de flexion d'un système peut être grossière estimée à partir de l'équation obtenue pour une plaque plane mince :
| (2.6) |
où
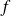est la fréquence, D est le module de rigidité de la structure et M la masse surfacique.
